|
Self-supervised relative depth learning for urban scene understanding (ECCV 2018)
[pdf]
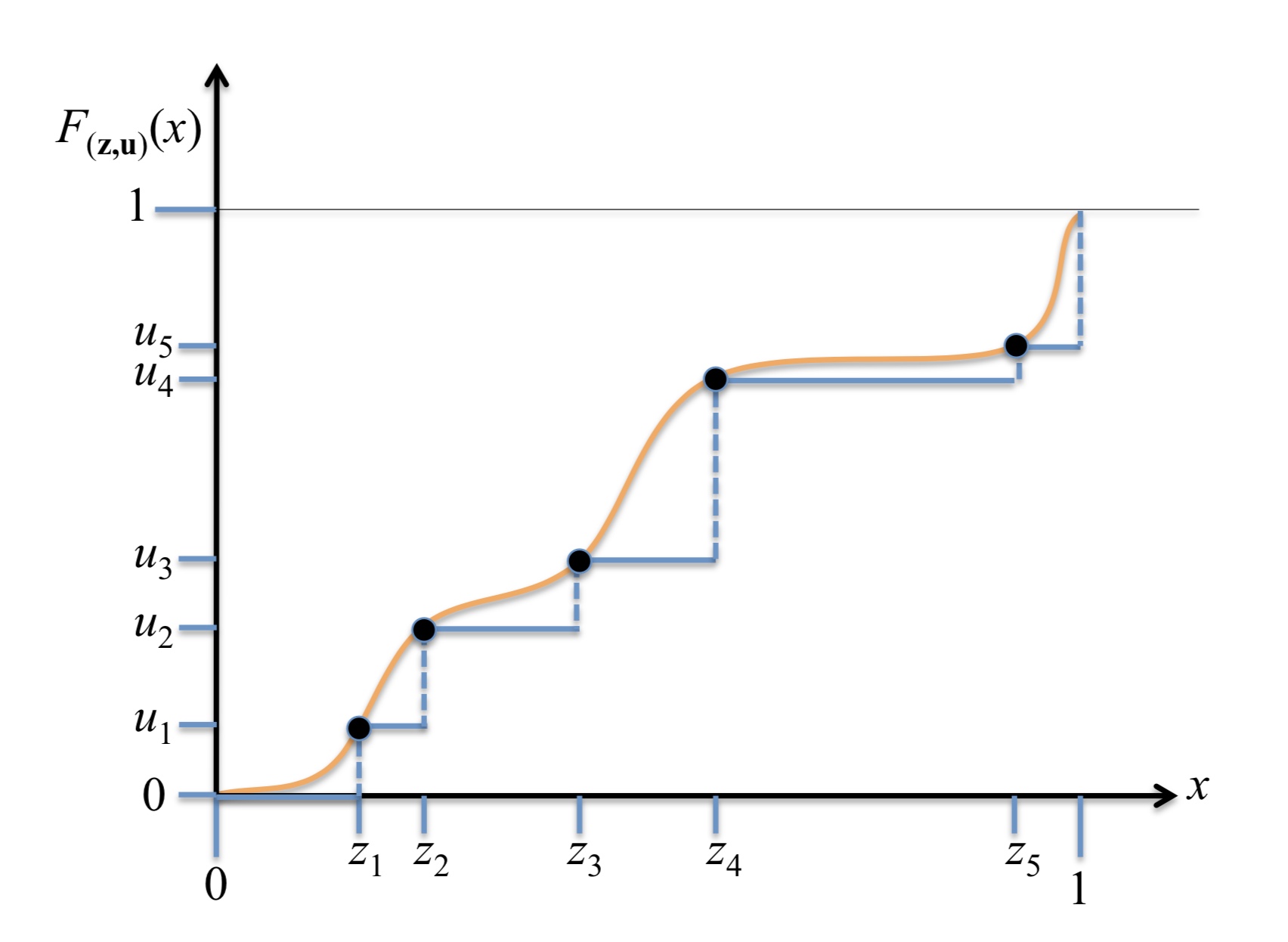
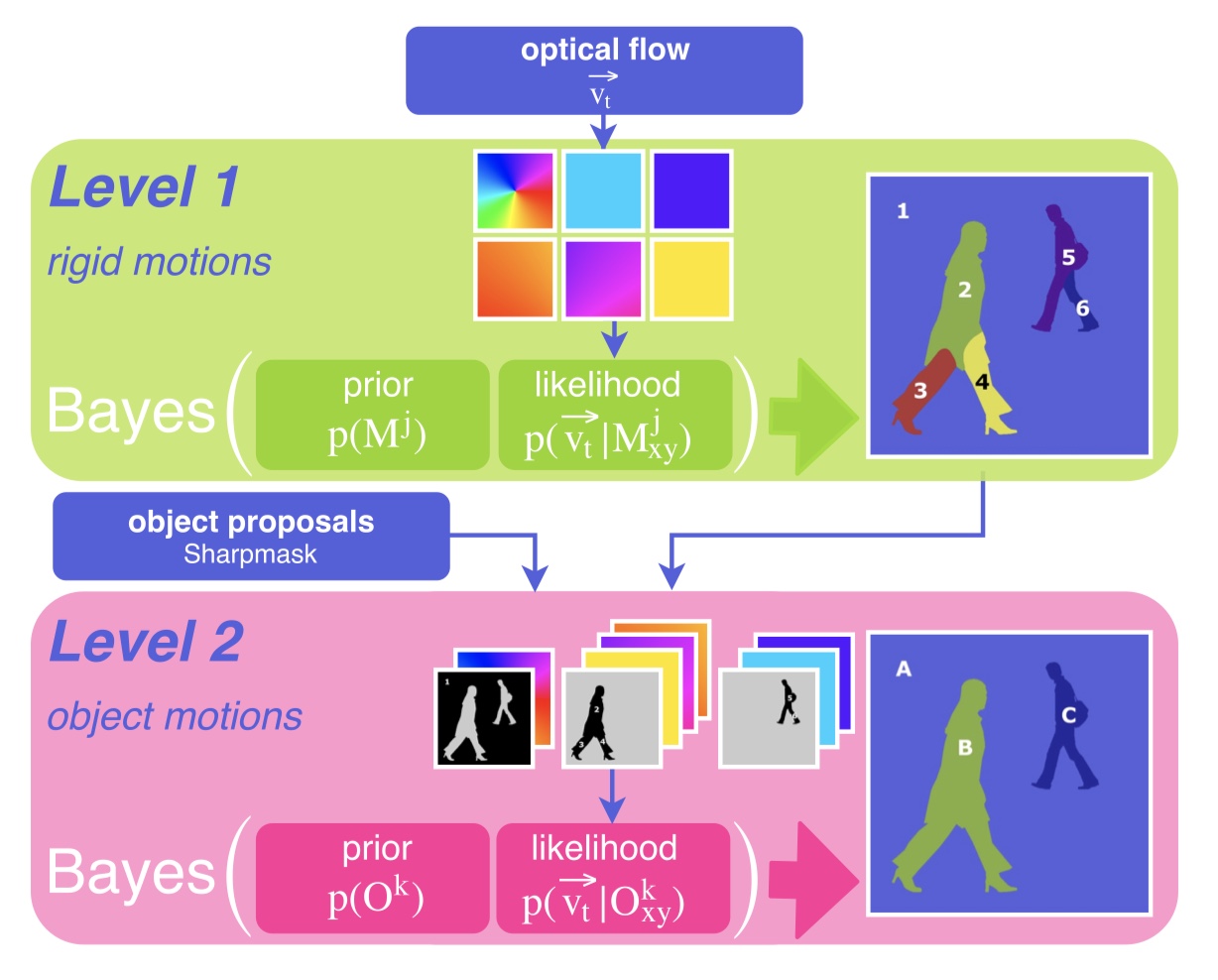
As an agent moves through the world, the apparent motion of scene elements is (usually) inversely proportional to their depth. It is natural for a learning agent to associate image patterns with the magnitude of their displacement over time: as the agent moves, faraway mountains don’t move much; nearby trees move a lot. This natural relationship between the appearance of objects and their motion is a rich source of information about the world. In this work, we start by training a deep network, using fully automatic supervision, to predict relative scene depth from single images. The relative depth training images are automatically derived from simple videos of cars moving through a scene, using recent motion segmentation techniques, and no human-provided labels. The proxy task of predicting relative depth from a single image induces features in the network that result in large improvements in a set of downstream tasks including semantic segmentation, joint road segmentation and car detection, and monocular (absolute) depth estimation, over a network trained from scratch. The improvement on the semantic segmentation task is greater than that produced by any other automatically supervised methods. Moreover, for monocular depth estimation, our unsupervised pre-training method even outperforms supervised pre-training with ImageNet. In addition, we demonstrate benefits from learning to predict (again, completely unsupervised) relative depth in the specific videos associated with various downstream tasks (e.g., KITTI). We adapt to the specific scenes in those tasks in an unsupervised manner to improve performance. In summary, for semantic segmentation, we present state-of-the-art results among methods that do not use supervised pre-training, and we even exceed the performance of supervised ImageNet pre-trained models for monocular depth estimation, achieving results that are comparable with state-of-the-art methods.
|