An Analysis of Surface Area Estimates of Binary Volumes Under Three Tilings
Introduction
To represent images or volumes in a digital computer, they must be discretized. This discretization leads to errors in the computation of such fundamental properties of objects as perimeter, area, volume, and surface area. Not surprisingly, the magnitudes of these errors depend upon the particular discretization used. There are an infinite variety of discrete approximations for any figure, from the spatial frequency decompositions used in signal processing to parameterized NURB surfaces used in the CAD/CAM world. In my thesis, I focussed on a particular class of discretizations: the tessellation of planar figures and solid volumes. Tessellations are approximate representations particularly convenient in computer vision and graphics.
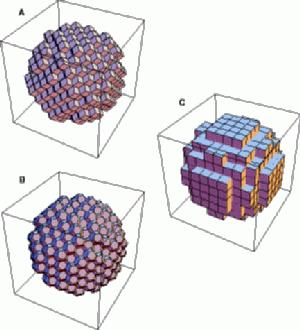
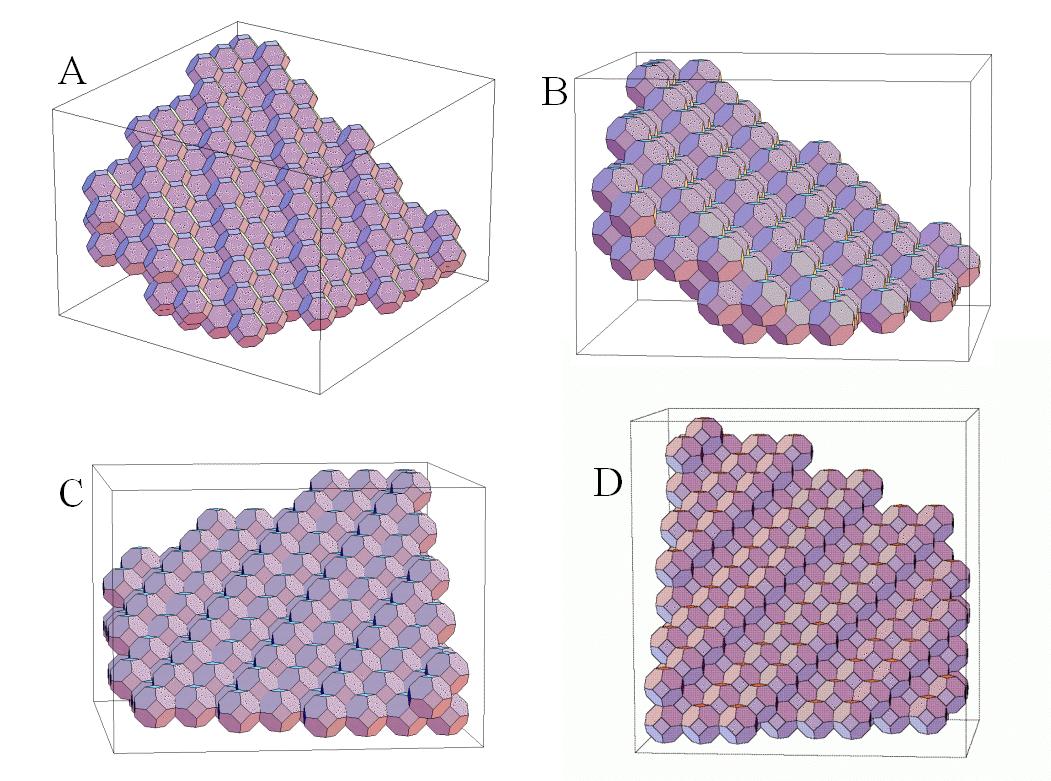
At right are three different ways of "tessellating" or "voxelizing" a sphere. Image A uses rhombic dodecahedra. Image B uses truncated octahedra. Image C uses regular rectangular prisms, also known as cubes. :)
I show in my thesis that for computing surface areas using local counting algorithms, estimates are more accurate and have less variance using the rhombic dodecahedron representations.
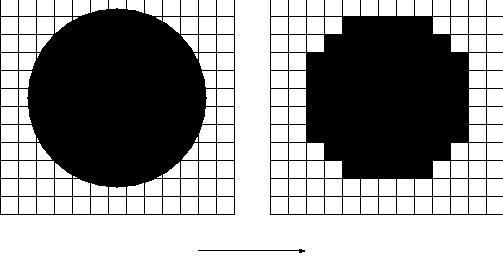
Counter-Intuitive Fact
Suppose we want to estimate the area of a smoothly bounded plane
figure such as the circle shown at left. One way would be to scan it into a computer, count
the number of pixels in the figure, and then multiply by the area of
each pixel. The error in our area estimate would be related to how
small
the pixels are. That is, if we use large pixels, we will incur error
on the boundary of our figure because the boundary is not well
represented
by the large pixels. It seems obvious that if we reduce the pixel size
enough that this process, in the limit, will give us the true area of
our plane figure.
However, suppose we want to compute the perimeter of a region by
adding the
length of the boundaries of all of the border pixels. While our
perimeter
estimate will improve to a certain extent as we make the pixels
smaller,
the surprising fact is that we cannot eliminate all of the
error by making the pixels arbitrarily small. This is easily seen
for the straight line example in the next image.
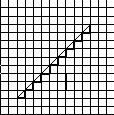
The "Manhattan Length" of a Line
At right we illustrate the local counting method for estimating the length of a 45 degree diagonal line. We merely add the length of the stairstep representations of the line. This clearly gives and overestimate of the true line length. Oddly enough, the estimate for the line length does not change (except for at the endpoints) as the pixel size is decreased. That is, the total length of the stairsteps remains constant with changes in pixel size.
This implies that using a local counting algorithm, we cannot obtain a more and more accurate perimeter estimate merely by increasing our resolution (at least in this case).
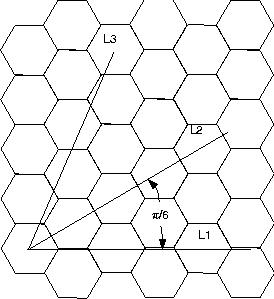
Hexagonal Grids
It turns out that by using hexagonal pixels, we can achieve a
mean error in perimeter estimates that is the same as for a square
grid, but with a much lower variance. Hence, local counting perimeter estimates of
smooth figures on an hexagonal grid are more reliable if the pixels
are "small."
3-D Tilings
In three dimensions, we have a situation very similar to that in two dimensions. We find that we can accurately estimate the volume of a smooth binary volume by merely making the voxels smaller and smaller. However, we run into the same problem with 3-D surface area as we did with perimeter in 2-D, i.e. we cannot accurately estimate surface area using local counting methods merely by making our voxels smaller.
Hence, I explored the benefits of using different voxel shapes. On the right are some examples of some planar patches represented with truncated octahedra.
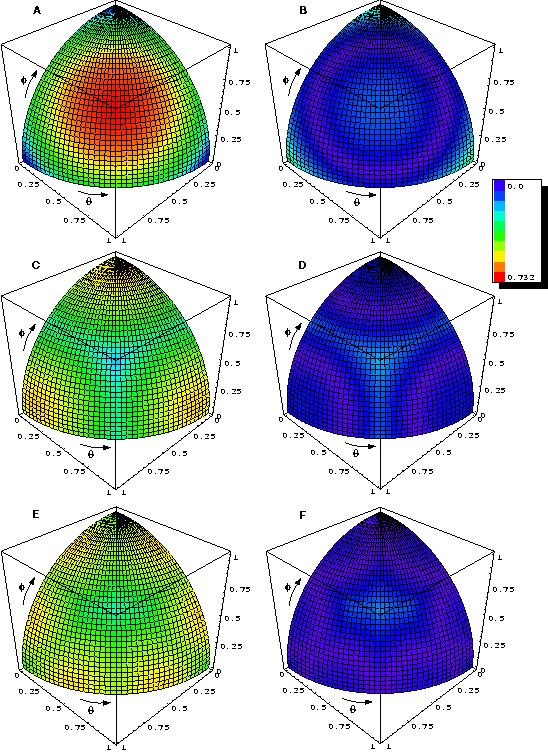
Results
On the left are six plots. The three on the far left show the error
in surface area estimates of a plane as a function of the azimuth and
declination of the plane.
A.The topmost of the far left plots is for
cubic voxels. Notice the large errors (in red) for planes which are not near
the
principal cartesian planes (x-z, y-z, x-y).
C. The middle far left plot is for the truncated octahedron voxel. Notice
that the maximum error is much smaller and that the variance in error
is
also smaller.
E. The lower left plot is for the rhombic dodecahedron voxel. This had
the smallest errors of all three voxel shapes, and hence, is
presumably
better for computing surface areas using local counting algorithms.
B,D,F. The plots on the right show errors for the same three voxel
shapes
after using a "correction factor". The rhombic dodecahedron shows
lower
errors after the correction is made as well.