
Justin Domke's Publications Click to hide abstracts
Divide and Couple: Using Monte Carlo Variational Objectives for Posterior Approximation J. Domke and D. Sheldon NeurIPS 2019 arxiv slides poster
Recent work in variational inference (VI) uses ideas from Monte Carlo estimation to tighten the lower bounds on the log-likelihood that are used as objectives. However, there is no systematic understanding of how optimizing different objectives relates to approximating the posterior distribution. Developing such a connection is important if the ideas are to be applied to inference-i.e., applications that require an approximate posterior and not just an approximation of the log-likelihood. Given a VI objective defined by a Monte Carlo estimator of the likelihood, we use a "divide and couple" procedure to identify augmented proposal and target distributions. The divergence between these is equal to the gap between the VI objective and the log-likelihood. Thus, after maximizing the VI objective, the augmented variational distribution may be used to approximate the posterior distribution.
Provable Gradient Variance Guarantees for Black-Box Variational Inference J. Domke NeurIPS 2019 arxiv poster
Recent variational inference methods use stochastic gradient estimators whose variance is not well understood. Theoretical guarantees for these estimators are important to understand when these methods will or will not work. This paper gives bounds for the common "reparameterization" estimators when the target is smooth and the variational family is a location-scale distribution. These bounds are unimprovable and thus provide the best possible guarantees under the stated assumptions.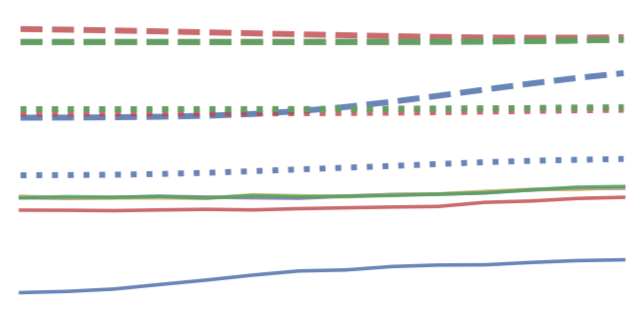
Thompson Sampling and Approximate Inference M. Phan, Y. Abbasi-Yadkori and J. Domke NeurIPS 2019 arxiv
We study the effects of approximate inference on the performance of Thompson sampling in the k-armed bandit problems. Thompson sampling is a successful algorithm for online decision-making but requires posterior inference, which often must be approximated in practice. We show that even small constant inference error (in α-divergence) can lead to poor performance (linear regret) due to under-exploration (for α<1) or over-exploration (for α>0) by the approximation. While for α>0 this is unavoidable, for α≤0 the regret can be improved by adding a small amount of forced exploration even when the inference error is a large constant.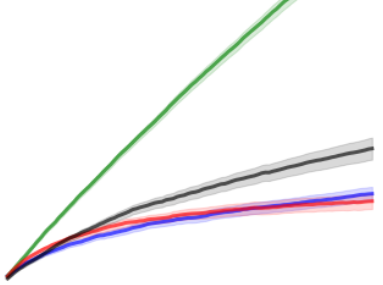
Provable Smoothness Guarantees for Black-Box Variational Inference J. Domke Arxiv 2019 arxiv
Black-box variational inference tries to approximate a complex target distribution through a gradient-based optimization of the parameters of a simpler distribution. Provable convergence guarantees require structural properties of the objective. This paper shows that for location-scale family approximations, if the target is M- Lipschitz smooth, then so is the “energy” part of the variational objective. The key proof idea is to describe gradients in a certain inner-product space, thus permitting the use of Bessel’s inequality. This result gives bounds on the location of the optimal parameters, and is a key ingredient for convergence guarantees.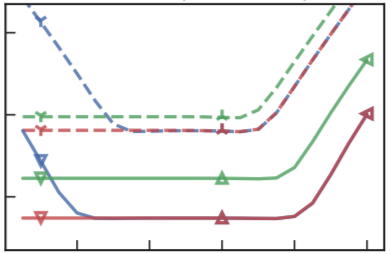
Using Large Ensembles of Control Variates forVariational Inference T. Geffner and J. Domke NeurIPS 2018 arxiv
Variational inference is increasingly being addressed with stochastic optimization. In this setting, the gradient's variance plays a crucial role in the optimization procedure, since high variance gradients lead to poor convergence. A popular approach used to reduce gradient's variance involves the use of control variates. Despite the good results obtained, control variates developed for variational inference are typically looked at in isolation. In this paper we clarify the large number of control variates that are available by giving a systematic view of how they are derived. We also present a Bayesian risk minimization framework in which the quality of a procedure for combining control variates is quantified by its effect on optimization convergence rates, which leads to a very simple combination rule. Results show that combining a large number of control variates this way significantly improves the convergence of inference over using the typical gradient estimators or a reduced number of control variates.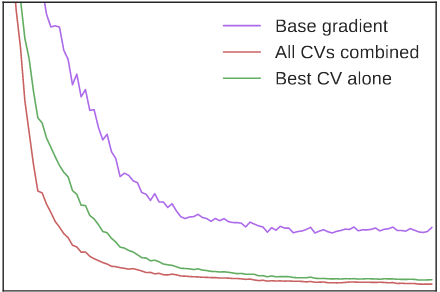
Importance Weighting and Variational Inference J. Domke and D. Sheldon NeurIPS 2018 arxiv poster
Recent work used importance sampling ideas for better variational bounds on likeli-hoods. We clarify the applicability of these ideas to pure probabilistic inference, byshowing the resulting Importance Weighted Variational Inference (IWVI) techniqueis an instance of augmented variational inference, thus identifying the looseness inprevious work. Experiments confirm IWVI’s practicality for probabilistic inference.As a second contribution, we investigate inference with elliptical distributions,which improves accuracy in low dimensions, and convergence in high dimensions.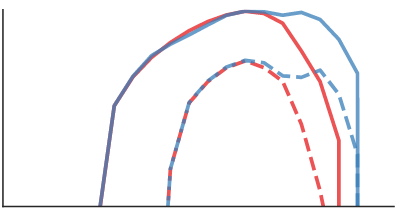
A Divergence Bound for Hybrids of MCMC and Variational Inference and an Application to Langevin Dynamics and SGVI J. Domke ICML 2017 pdf slides poster blog
Two popular classes of methods for approximate inference are Markov chain Monte Carlo (MCMC) and variational inference. MCMC tends to be accurate if run for a long enough time, while variational inference tends to give better approximations at shorter time horizons. However, the amount of time needed for MCMC to exceed the performance of variational methods can be quite high, motivating more fine-grained tradeoffs. This paper derives a distribution over variational parameters, designed to minimize a bound on the divergence between the resulting marginal distribution and the target, and gives an example of how to sample from this distribution in a way that interpolates between the behavior of existing methods based on Langevin dynamics and stochastic gradient variational inference (SGVI).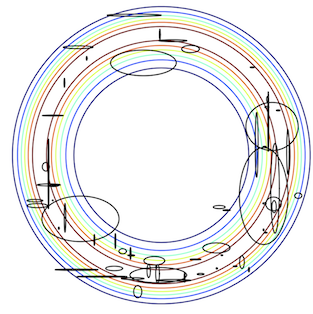
Distributed Solar Prediction with Wind Velocity J. Domke, N. Engerer, A. Menon and C. Webers IEEE Photovoltaic Specialists Conference (PVSC) 2016
The growing uptake of residential PV (photovoltaic) systems creates challenges for electricity grid management, owing to the fundamentally intermittent nature of PV production. This creates the need for PV forecasting based on a distributed network of sites, which has been an area of active research in the past few years. This paper describes a new statistical approach to PV forecasting, with two key contributions. First, we describe a "local regularisation" scheme, wherein the PV energy at a given site is only attempted to be predicted based on measurements on geographically nearby sites. Second, we describe a means of incorporating wind velocities into our prediction, which we term "wind expansion", and show that this scheme is robust to errors in specification of the velocities. Both these extensions are shown to significantly improve the accuracy of PV prediction.
Clamping Improves TRW and Mean Field Approximations A. Weller and J. Domke AISTATS 2016 arxiv
We examine the effect of clamping variables for approximate inference in undirected graphical models with pairwise relationships and discrete variables. For any number of variable labels, we demonstrate that clamping and summing approximate sub-partition functions can lead only to a decrease in the partition function estimate for TRW, and an increase for the naive mean field method, in each case guaranteeing an improvement in the approximation and bound. We next focus on binary variables, add the Bethe approximation to consideration and examine ways to choose good variables to clamp, introducing new methods. We show the importance of identifying highly frustrated cycles, and of checking the singleton entropy of a variable. We explore the value of our methods by empirical analysis and draw lessons to guide practitioners.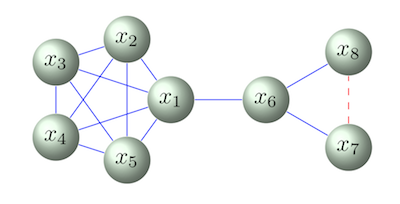
Reflection, Refraction, and Hamiltonian Monte Carlo H. Afshar and J. Domke NIPS 2015 pdf
Hamiltonian Monte Carlo (HMC) is a successful approach for sampling from continuous densities. However, it has difficulty simulating Hamiltonian dynamics with non-smooth functions, leading to poor performance. This paper is motivated by the behavior of Hamiltonian dynamics in physical systems like optics. We introduce a modification of the Leapfrog discretization of Hamiltonian dynamics on piecewise continuous energies, where intersections of the trajectory with discontinuities are detected, and the momentum is reflected or refracted to compensate for the change in energy. We prove that this method preserves the correct stationary distribution when boundaries are affine. Experiments show that by reducing the number of rejected samples, this method improves on traditional HMC.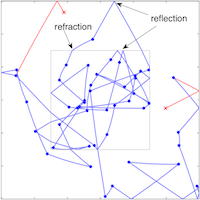
Maximum Likelihood Learning With Arbitrary Treewidth via Fast-Mixing Parameter Sets J. Domke NIPS 2015 pdf
Inference is typically intractable in high-treewidth undirected graphical models, making maximum likelihood learning a challenge. One way to overcome this is to restrict parameters to a tractable set, most typically the set of tree-structured parameters. This paper explores an alternative notion of a tractable set, namely a set of "fast-mixing parameters" where Markov chain Monte Carlo (MCMC) inference can be guaranteed to quickly converge to the stationary distribution. While it is common in practice to approximate the likelihood gradient using samples obtained from MCMC, such procedures lack theoretical guarantees. This paper proves that for any exponential family with bounded sufficient statistics, (not just graphical models) when parameters are constrained to a fast-mixing set, gradient descent with gradients approximated by sampling will approximate the maximum likelihood solution inside the set with high-probability. When unregularized, to find a solution ε-accurate in log-likelihood requires a total amount of effort cubic in 1/ε, disregarding logarithmic factors. When ridge-regularized, strong convexity allows a solution ε-accurate in parameter distance with an effort quadratic in 1/ε. Both of these provide of a fully-polynomial time randomized approximation scheme.
Loss-Calibrated Monte Carlo Action Selection E. Abbasnejad, J. Domke and S. Sanner AAAI 2015 pdf
Bayesian decision-theory underpins robust decision- making in applications ranging from plant control to robotics where hedging action selection against state uncertainty is critical for minimizing low probability but potentially catastrophic outcomes (e.g, uncontrollable plant conditions or robots falling into stairwells). Unfortunately, belief state distributions in such settings are often complex and/or high dimensional, thus prohibiting the efficient application of analytical techniques for expected utility computation when real-time control is required. This leaves Monte Carlo evaluation as one of the few viable (and hence frequently used) techniques for online action selection. However, loss-insensitive Monte Carlo methods may require large numbers of samples to identify optimal actions with high certainty since they may sample from high probability regions that do not disambiguate action utilities. In this paper we remedy this problem by deriving an optimal proposal distribution for a loss-calibrated Monte Carlo importance sampler that maximizes a lower bound on the expected utility of the best action. Empirically, we show that using our loss-calibrated Monte Carlo method yields high-accuracy optimal action selections in a fraction of the number of samples required by conventional loss-insensitive samplers.
Projecting Markov Random Fields for Fast Mixing X. Liu and J. Domke NIPS 2014 pdf
Markov chain Monte Carlo (MCMC) algorithms are simple and extremely powerful techniques to sample from almost arbitrary distributions. The flaw in practice is that it can take a large and/or unknown amount of time to converge to the stationary distribution. This paper gives sufficient conditions to guarantee that univariate Gibbs sampling on Markov Random Fields (MRFs) will be fast mixing, in a precise sense. Further, an algorithm is given to project onto this set of fast-mixing parameters in the Euclidean norm. Following recent work, we give an example use of this to project in various divergence measures, comparing univariate marginals obtained by sampling after projection to common variational methods and Gibbs sampling on the original parameters.
Finito: A Faster, Permutable Incremental Gradient Method for Big Data Problems A. Defazio, T. Caetano and J. Domke ICML 2014 pdf talk
Recent advances in optimization theory have shown that smooth strongly convex finite sums can be minimized faster than by treating them as a black box "batch" problem. In this work we introduce a new method in this class with a theoretical convergence rate four times faster than existing methods, for sums with sufficiently many terms. This method is also amendable to a sampling without replacement scheme that in practice gives further speed-ups. We give empirical results showing state of the art performance.
Training Structured Predictors Through Iterated Logistic Regression J. Domke Advanced Structured Prediction, MIT Press, 2014 pdf talk
In a setting where approximate inference is necessary, structured learning can be formulated as a joint optimization of inference "messages" and local potentials. This chapter observes that, for fixed messages, the optimization problem with respect to potentials takes the form of a logistic regression problem, biased by the current set of messages. This observation leads to an algorithm that alternates between message-passing inference updates, and learning updates. It is possible to employ any set of potential functions where an algorithm exists to optimize a logistic loss, including linear functions, boosted decision trees, and multi-layer perceptrons.
Structured Learning via Logistic Regression J. Domke NIPS 2013 pdf
A successful approach to structured learning is to write the learning objective as a joint function of linear parameters and inference messages, and iterate between updates to each. This paper observes that if the inference problem is "smoothed" through the addition of entropy terms, for fixed messages, the learning objective reduces to a traditional (non-structured) logistic regression problem with respect to parameters. In these logistic regression problems, each training example has a bias term determined by the current set of messages. Based on this insight, the structured energy function can be extended from linear factors to any function class where an "oracle" exists to minimize a logistic loss.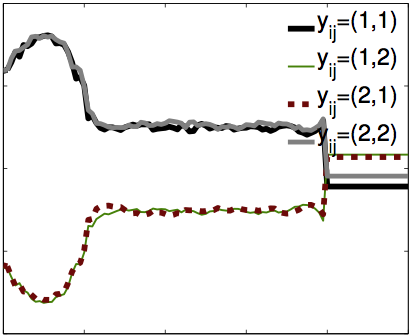
Projecting Ising Model Parameters for Fast Mixing J. Domke and X. Liu NIPS 2013 pdf code
Inference in general Ising models is difficult, due to high treewidth making tree-based algorithms intractable. Moreover, when interactions are strong, Gibbs sampling may take exponential time to converge to the stationary distribution. We present an algorithm to project Ising model parameters onto a parameter set that is guaranteed to be fast mixing, under several divergences. We find that Gibbs sampling using the projected parameters is more accurate than with the original parameters when interaction strengths are strong and when limited time is available for sampling.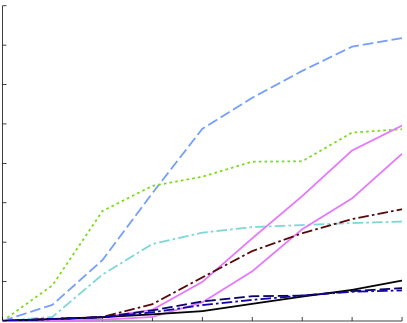
Learning Graphical Model Parameters with Approximate Marginals Inference J. Domke PAMI 2013 pdf talk
Likelihood based-learning of graphical models faces challenges of computational-complexity and robustness to model mis-specification. This paper studies methods that fit parameters directly to maximize a measure of the accuracy of predicted marginals, taking into account both model and inference approximations at training time. Experiments on imaging problems suggest marginalization-based learning performs better than likelihood-based approximations on difficult problems where the model being fit is approximate in nature.
Generic Methods for Optimization-Based Modeling J. Domke AISTATS 2012 pdf code
"Energy" models for continuous domains can be applied to many problems, but often suffer from high computational expense in training, due to the need to repeatedly minimize the energy function to high accuracy. This paper considers a modified setting, where the model is trained in terms of results after optimization is truncated to a fixed number of iterations. We derive "backpropagating" versions of gradient descent, heavy-ball and LBFGS. These are simple to use, as they require as input only routines to compute the gradient of the energy with respect to the domain and parameters. Experimental results on denoising and image labeling problems show that learning with truncated optimization greatly reduces computational expense compared to "full" fitting.
Dual Decomposition for Marginal Inference J. Domke AAAI 2011 pdf slides
We present a dual decomposition approach to the tree-reweighted belief propagation objective. Each tree in the tree-reweighted bound yields one subproblem, which can be solved with the sum-product algorithm. The master problem is a simple differentiable optimization, to which a standard optimization method can be applied. Experimental results on 10x10 Ising models show the dual decomposition approach using L-BFGS is similar in settings where message-passing converges quickly, and one to two orders of magnitude faster in settings where message-passing requires many iterations, specifically high accuracy convergence, and strong interactions.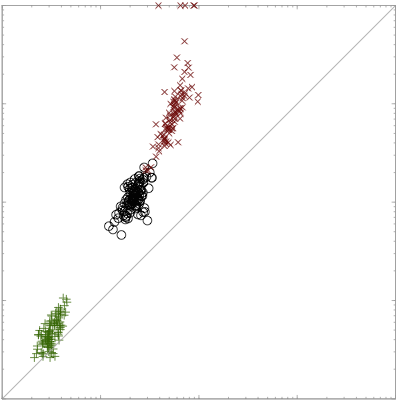
Parameter Learning with Truncated Message-Passing J. Domke CVPR 2011 pdf appendix
Training of conditional random fields often takes the form of a double-loop procedure with message-passing inference in the inner loop. This can be very expensive, as the need to solve the inner loop to high accuracy can require many message-passing iterations. This paper seeks to reduce the expense of such training, by redefining the training objective in terms of the approximate marginals obtained after message-passing is "truncated" to a fixed number of iterations. An algorithm is derived to efficiently compute the exact gradient of this objective. On a common pixel labeling benchmark, this procedure improves training speeds by an order of magnitude, and slightly improves inference accuracy if a very small number of message-passing iterations are used at test time.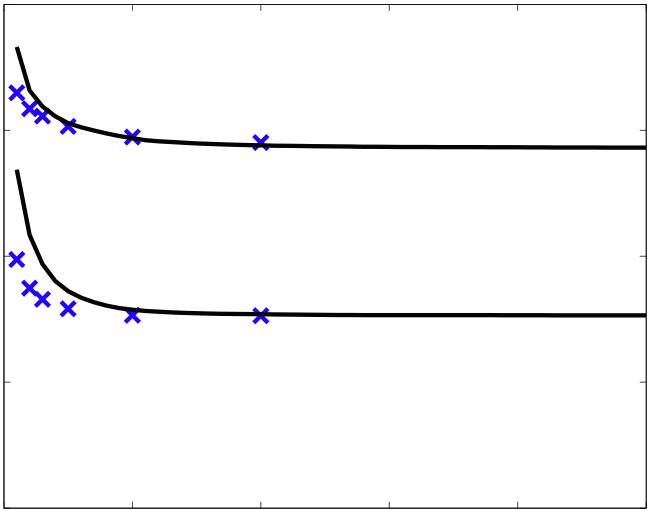
Implicit Differentiation by Perturbation J. Domke NIPS 2010 pdf
This paper proposes a simple and efficient finite difference method for implicit differentiation of marginal inference results in discrete graphical models. Given an arbitrary loss function, defined on marginals, we show that the derivatives of this loss with respect to model parameters can be obtained by running the inference procedure twice, on slightly perturbed model parameters. This method can be used with approximate inference, with a loss function over approximate marginals. Convenient choices of loss functions make it practical to fit graphical models with hidden variables, high treewidth and/or model misspecification.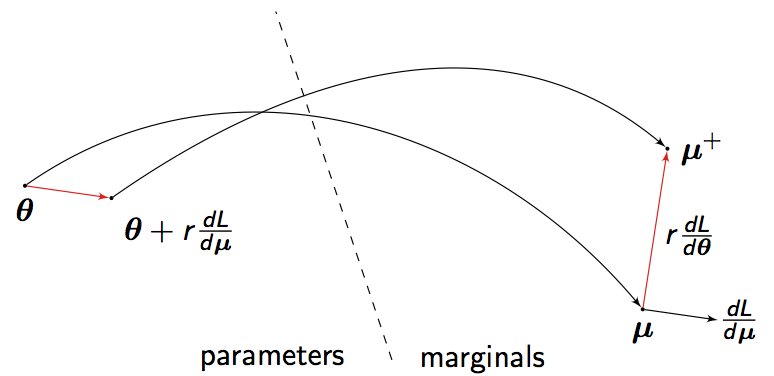
Image Transformations and Blurring J. Domke and Y. Aloimonos PAMI 2009 pdf
Since cameras blur the incoming light during measurement, different images of the same surface do not contain the same information about that surface. Thus, in general, corresponding points in multiple views of a scene have different image intensities. While multiple view geometry constrains the locations of corresponding points, it does not give relationships between the signals at corresponding locations. This paper offers an elementary treatment of these relationships. We first develop the notion of "ideal" and "real" images, corresponding to, respectively, the raw incoming light and the measured signal. This framework separates the filtering and geometric aspects of imaging. We then consider how to synthesize one view of a surface from another; if the transformation between the two views is affine, it emerges that this is possible if and only if the singular values of the affine matrix are positive. Next, we consider how to combine the information in several views of a surface into a single output image. By developing a new tool called "frequency segmentation" we show how this can be done despite not knowing the blurring kernel.
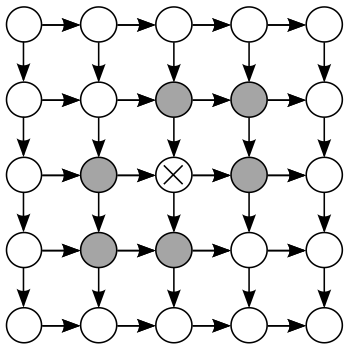
Who Killed the Directed Model? J. Domke, A. Karapurkar and Y. Aloimonos CVPR 2008 pdf
Prior distributions are useful for robust low-level vision, and undirected models (e.g. Markov Random Fields) have become a central tool for this purpose. Though sometimes these priors can be specified by hand, this becomes difficult in large models, which has motivated learning these models from data. However, maximum likelihood learning of undirected models is extremely difficult- essentially all known methods require approximations and/or high computational cost. Conversely, directed models are essentially trivial to learn from data, but have not received much attention for low-level vision. We compare the two formalisms of directed and undirected models, and conclude that there is no a priori reason to believe one better represents low-level vision quantities. We formulate two simple directed priors, for natural images and stereo disparity, to empirically test if the undirected formalism is superior. We find in both cases that a simple directed model can achieve results similar to the best learnt undirected models with significant speedups in training time, suggesting that directed models are an attractive choice for tractable learning.
Learning Convex Inference of Marginals J. Domke UAI 2008 pdf talk
Graphical models trained using maximum likelihood are a common tool for probabilistic inference of marginal distributions. However, this approach suffers difficulties when either the inference process or the model is approximate. In this paper, the inference process is first defined to be the minimization of a covex fnuction, inspired by free energy approximations. Learning is then done directly in terms of the performance of the inference process at univariate marginal prediction. The main novelty is that this is a direct minimization of empirical risk, where the risk measures the accuracy of predicted marginals.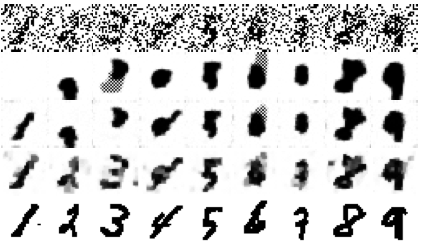
Signals on Pencils of Lines J. Domke and Y. Aloimonos ICCV 2007 pdf
This paper proposes the "epipolar pencil transformation" (EPT). This is a tool for comparing the signals in different images, with no use of feature detection, yet taking advantage of the constraints given by epipolar geometry. The idea is to develop a descriptor for each point, summarizing the signals on the pencil of lines intersecting at that point. To compute the EPT, first find compact descriptors for each line, then combine these appropriately for each pencil. Given the EPT for two images, computing the epipolar geometry reduces to a closest pairs problem- select one pencil from each set such that the L1 distance (in descriptor space) is minimized. By this reduction to a high dimensional closest pairs problem, recent advances in computational geometry can be used to efficiently identify the best global solution. This technique is robust, as each potential solution is evaluated by comparing the signals for all the lines passing through the two hypothesized epipoles. At the same time, as the closest pairs algorithm performs a global search, the solution is not distracted by local minima. The EPT is used here both for the problem of two-view rigid motion, and many-view place recognition.
Multiple View Image Reconstruction: A Harmonic Approach J. Domke and Y. Aloimonos CVPR 2007 pdf
This paper presents a new constraint connecting the signals in multiple views of a surface. The constraint arises from a harmonic analysis of the geometry of the imaging process and it gives rise to a new technique for multiple view image reconstruction. Given several views of a surface from different positions, fundamentally different information is present in each image, owing to the fact that cameras measure the incoming light only after the application of a low-pass filter. Our analysis shows how the geometry of the imaging is connected to this filtering. This leads to a technique for constructing a single output image containing all the information present in the input images.
A Probabilistic Notion of Camera Geometry: Calibrated vs. Uncalibrated J. Domke and Y. Aloimonos PCV 2006 pdf
We suggest altering the fundamental strategy in Fundamental or Essential Matrix estimation. The traditional approach first estimates correspondences, and then estimates the camera geometry on the basis of those correspondences. Though the second half of this approach is very well developed, such algorithms often fail in practice at the correspondence step. Here, we suggest altering the strategy. First, estimate probability distributions of correspondence, and then estimate camera geometry directly from these distributions. This strategy has the effect of making the correspondence step far easier, and the camera geometry step somewhat harder. The success of our approach hinges on if this trade-off is wise. We will present an algorithm based on this strategy. Fairly extensive experiments suggest that this trade-off might be profitable.
Deformation and Viewpoint Invariant Color Histograms J. Domke and Y. Aloimonos BMVC 2006 pdf
We develop a theoretical basis for creating color histograms that are invariant under deformation or changes in viewpoint. The gradients in different color channels weight the influence of a pixel on the histogram so as to cancel out the changes induced by deformations. Experiments show these histograms to be invariant under a variety of distortions and changes in viewpoint.
A Probabilistic Notion of Correspondence and the Epipolar Constraint J. Domke and Y. Aloimonos 3DPVT 2006 pdf
We present a probabilistic framework for correspondence and egomotion. First, we suggest computing probability distributions of correspondence. This has the advantage of being robust to points subject to the aperture effect and repetitive structure, while giving up no information at feature points. Additionally, correspondence probability distributions can be computed for every point in the scene. Next, we generate a probability distribution over the motions, from these correspondence probability distributions, through a probabilistic notion of the epipolar constraint. Finding the maximum in this distribution is shown to be a generalization of least-squared epipolar minimization. We will show that because our technique allows so much correspondence information to be extracted, more accurate egomotion estimation is possible.
Integration of Visual and Inertial Information for Egomotion: a Stochastic Approach J. Domke and Y. Aloimonos ICRA 2006 pdf
We present a probabilistic framework for visual correspondence, inertial measurements and Egomotion. First, we describe a simple method based on Gabor filters to produce correspondence probability distributions. Next, we generate a noise model for inertial measurements. Probability distributions over the motions are then computed directly from the correspondence distributions and the inertial measurements. We investigate combining the inertial and visual information for a single distribution over the motions. We find that with smaller amounts of correspondence information, fusion of the visual data with the inertial sensor results in much better Egomotion estimation. This is essentially because inertial measurements decrease the "translation-rotation" ambiguity. However, when more correspondence information is used, this ambiguity is reduced to such a degree that the inertial measurements provide negligible improvement in accuracy. This suggests that inertial and visual information are more closely integrated in a compositional sense.
A Probabilistic Framework for Correspondence and Egomotion J. Domke and Y. Aloimonos ICCV WDV 2005 pdf
This paper is an argument for two assertions: First, that by representing correspondence probabilistically, drastically more correspondence information can be extracted from images. Second, that by increasing the amount of correspondence information used, more accurate egomotion estimation is possible. We present a novel approach illustrating these principles. We first present a framework for using Gabor filters to generate such correspondence probability distributions. Essentially, different filters 'vote' on the correct correspondence in a way giving their relative likelihoods. Next, we use the epipolar constraint to generate a probability distribution over the possible motions. As the amount of correspondence information is increased, the set of motions yielding significant probabilities is shown to "shrink" to the correct motion.