Poster Gallery:
Data Sets:
C O D E: GGMGwishart v1.0
Description: The GGMGwishart v1.0 MATLAB code package implements several marginal likelihood approximation methods for non-decomposable Gaussian Graphical Models (GGMs) under a G-Wishart prior. The methods are described in our NIPS 2009 paper. The approximations include BIC score, Laplace approximation, diagonal Hessian Laplace approximation, and the Monte Carlo estimator of Atay-Kayis and Massam.Download: GGMGWishart.zip (430KB)
Package Contents: The main files in included in this package are:
-
GGMGWExample.m: runs each method on the Iris Virginica example described in
Atay-Kayis and Massam [2, p. 333, Figure 3]. See below for sample output from
this example.
-
GGMGWScore.m: common wrapper function that computes the score (marginal
likelihood approximation) using any of the four methods (BIC, Laplace,
diagonal Hessian Laplace, and Monte Carlo).
-
GGMGWFit.m: code for finding the posterior mode of the precision matrix under
a G-Wishart prior given a graph structure and data matrix.
Used by BIC and Laplace methods.
-
This package requires MATLAB.
It has been tested using both 32bit and 64bit versions of MATLAB 7.8+
on Linux and Windows platforms. If you have any trouble running the code
please contact me.
-
This package depends on Mark Schmidt's freely available
minFunc
optimization package. minFunc must be installed and on the MATLAB path for
this package to work.
-
The Monte Carlo estimation code is implemented as a C++ mex file. The mex
code has been verified to compile correctly under the gcc and MS Visual
Studio 2008 compilers on Linux and Windows, and mex binaries are included. Use
of other platforms and compilers may require changes to the make file. The
C++ mex code is based on code released by
Mike West's group at Duke.
Note that our code only provides a mex interface for the marginal likelihood
computation.
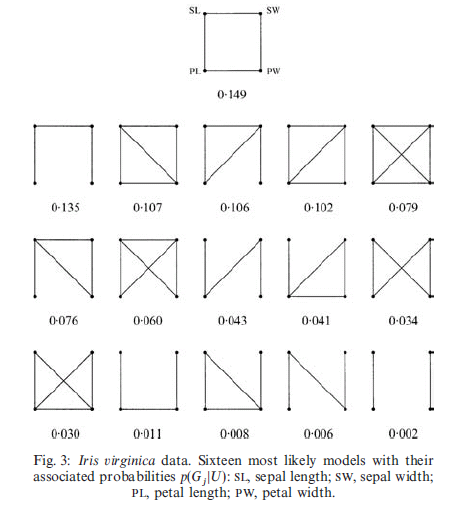
Figure 1: Graphs and posterior probabilities for the top 16 graphs as computed by Atay-Kayis and Massam.
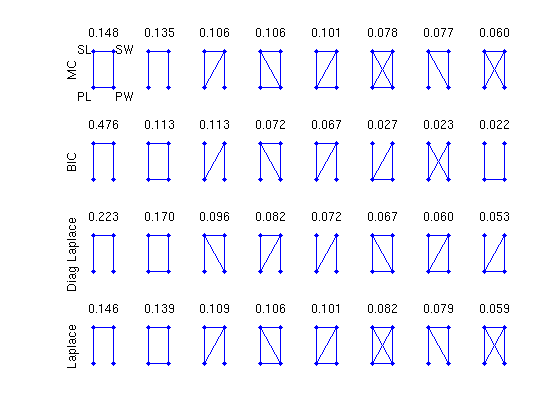
Figure 2: Graphs and posterior probabilities for the four methods included in this code package. MC is the Monte Carlo method of Atay-Kayis and Massam. The MC results are very close to those given in Atay-Kayis and Massam.
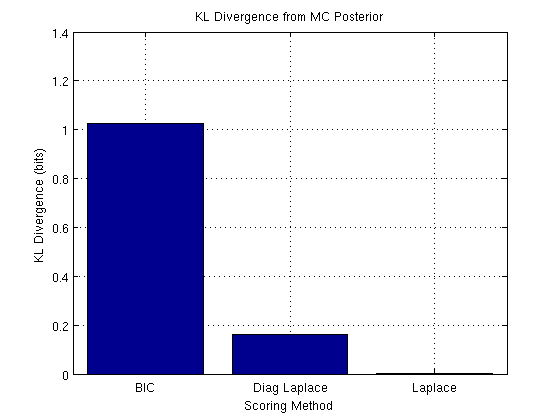
Figure 3: KL divergence from the Monte Carlo posterior over graphs to the posteriors compute from BIC, diagonal Hessian Laplace, and Laplace marginal likelihood approximations. We see that Laplace is more accurate than diagonal Laplace, which is more accurate than BIC.
This site last updated March 3, 2014. © Benjamin M. Marlin





