This assignment is due at 1700 on Friday, 10 October Friday, 17 October.

The goal of this problem is to implement a solver for Kakuro. Kakuro is a logic puzzle similar to Sudoku.

I will be updating the assignment with questions (and their answers) as they are asked.

See also the Assignment 04 Template.

Problem

Kakuro is a logic puzzle played on a grid. The grid cells are similar to a crossword puzzle: some are filled and some are open. Some filled cells contain clues, which relate either to a column or row of cells adjacent to that filled cell.

The goal of Kakuro is to fill the open cells with the numbers 1–9 such that

• the numbers in a given row or column total to the clue in the filled cell to the left of the row or above the column; and
• no number is repeated in any contiguous row or column of cells (filled cells break up rows and columns and repeats can occur in aligned but non-contiguous columns)

For example, here is a Kakuro board:

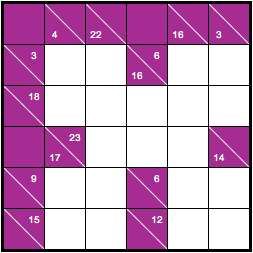
In this board, for example, the first open row (adjacent to the clue 3) must contain a 1 and a 2, since 1 + 2 = 3, and no other pair of distinct, valid digits sums to 3. But search or more inference is required to figure out which value ends up in which cell.

This is a brief overview; Wikipedia’s entry on Kakuro and numerous sites online have more details.

Input data format

We will test your program using data in the following text-based format.

The first line of input will list the width and height of the board, represented as a pair of whitespace-delimited integers. For example, a board seven cells across and five cells high will have a first line of:

1

7 5

The example puzzle shown above is six by six, and its representation would start with

1

6 6

Next, a list of clues and filled spaces is given. The list is not in any particular order. Each element of the list is on its own line, and consists of four whitespace-delimited elements. They are, in order:

• The rightward horizontal offset from the top left cell; in other words, the x-position, given that the upper-left cell is (0,0), as an integer.
• The vertical offset from the top left cell, as an integer.
• If the element is a clue:
  • Then whether the clue is for the adjacent horizontal row to the right, denoted by an h, or vertical column below, denoted by a v.
  • Otherwise, an x, denoting a filled space.
• The integer value of the clue, or 0 if it is a filled space.

The example puzzle shown above might be represented as:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

6 6
0 0 x 0
1 0 v 4
2 0 v 22
3 0 x 0
4 0 v 16
5 0 v 3
0 1 h 3
3 1 h 6
3 1 v 16
0 2 h 18
0 3 x 0
1 3 h 23
1 3 v 17
5 3 v 14
0 4 h 9
3 4 h 6
0 5 h 15
3 5 h 12

(Please email me if you notice any mistakes or inconsistencies.)

Output data format

Your program’s output should be a sequence of lines, one per open cell in the original puzzle. Each line should contain three whitespace-separated values that locate the cell and describe the value that it should contain in the solution:

• The rightward horizontal offset from the top left cell; in other words, the x-position, given that the upper-left cell is (0,0), as an integer.
• The vertical offset from the top left cell, as an integer.
• The value of the digit placed in that cell, as an integer, in the range [1, 9].

For example, if we inferred in the puzzle above that the upper leftmost open cell should be 1, that would be represented by the line:

1

1 1 1

A full solution for the example will have twenty lines, one for each open cell.

What to submit

You should submit two things: a Kakuro solver and a readme.txt.

• Your solver should use its first command line argument as the path to an input file. If, for example, your solver’s main method is in a Java class named KakuroSolver, we should be able to use java KakuroSolver /Users/liberato/testcase to direct your program to read the input in the file located at /Users/liberato/testcase.
• Your solver should print the solved board to standard output, in exactly the format described above. Kakuro puzzles traditionally have a single, unique solution. Your program should find a solution and stop; it need not check that the solution in unique.

Submit the source code of your solver, written in the language of your choice. Name the file containing the main() method KakuroSolver.java or your language’s equivalent. If the file you submit depends upon other files, be sure to submit these other files as well.

As in the previous assignment, while you may use library calls for data structures and the like, you must implement the search method you use yourself. Do not use a library for search or constraint satisfaction. We will consider it plagiarism if you do. Check with us if you think there’s any ambiguity.

Your readme.txt should contain the following items:

• your name
• if the language of your choice is not Java, Python, Ruby, node.js-compatible JavaScript, ANSI C or C++ (or if you’re concerned it’s not completely obvious to us how to compile and execute it), a description of how to compile and execute the submitted files
• a list of which optimizations or heuristics, if any, you implemented (e.g., MRV, forward checking, AC-3, etc.)
• a description of what you got working, what is partially working and what is completely broken

If you’re using language features that require a specific version of your language or runtime, check for that version at program start and fail if it’s not present, emitting an understandable error message indicating this fact. Your program must compile and execute on the Edlab Linux machines.

If your program does not compile or execute, you will receive no credit. Check with us in advance if you’re concerned.

Grading

We will run your program on a variety of test cases. The exact test cases will not be available to you before grading, but we will post at least one sample in the correct format before the due date. You are welcome to write and distribute your own test cases (or test case generators).

If your readme.txt is missing or judged insufficient, your overall score may be penalized by up to ten percent.

We’re not going to feed your program incorrectly formatted input, so you need only concern yourself with handling input in the format described in the assignment. Further, each input puzzle we provide will be solvable.

We expect valid output. Generating output that is not in the format described in the assignment will result in a failed test case.

Some of the test cases may push at the boundaries of what your program will be capable of, depending upon your choice of search strategy. If your program exceeds available heap memory (which we’ll set to 1 GB in Java, using the -Xmx1024M argument if necessary), or if it does not terminate in twenty seconds, we will consider the test case failed.

Advice

As usual, a validator and/or visualizer for solutions will be useful. Even if you don’t write one, think about how you would. Many of the same techniques will apply when you’re implementing your own constraint checking system.

As is the case in many CSPs, using DFS alone will not be sufficient for non-trivial Kakuro puzzles. But you will find they fall relatively easily to a modicum of inference. Start with backtracking DFS and forward checking and see how far they get you.

You may consider a local search, as described in Section 6.4 of Russell and Norvig. I think this plan might be bad. Local search for CSPs works best when there are many possible satisfying assignments and few plateaux. This problem doesn’t fit those criteria, though a smart heuristic choice and additional techniques (tabu search, constraint weighting) will probably overcome this fact. But I could be wrong, and local search might be great — I haven’t tried a local search on Kakuro myself.

You may find it helpful to start by enumerating the valid values for each clue, given the length of the row or column adjacent cells. For example, a clue of 3 will always be adjacent to two open cells, which can only contain a 1 or 2. Be smart about your enumeration of possibilities for each clue/length combination, and/or hardcode it into either your program or a data file your program reads on startup.

Think carefully about your program’s representations. For example, if you plan to implement forward checking, the contents of a cell might better be represented by the set of remaining possible values, rather than the currently assigned value. Giving the problem and your approach some thought (“hammock time”) before you start coding will save you time in the long run.

Questions and answers

Should the lines be in a specific order? ie. lowest numbers first in x digit, then sorted by lowest numbers first in y digit? Or does it not matter?

It does not matter.