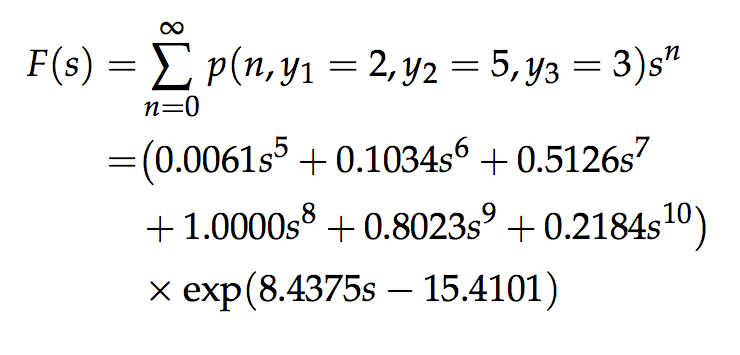
| Sponsor: | National Science Foundation |
| Principal Investigator: | Daniel Sheldon |
| Research Assistants: | Kevin Winner, Garrett Bernstein, Tao Sun, Debora Sujono |

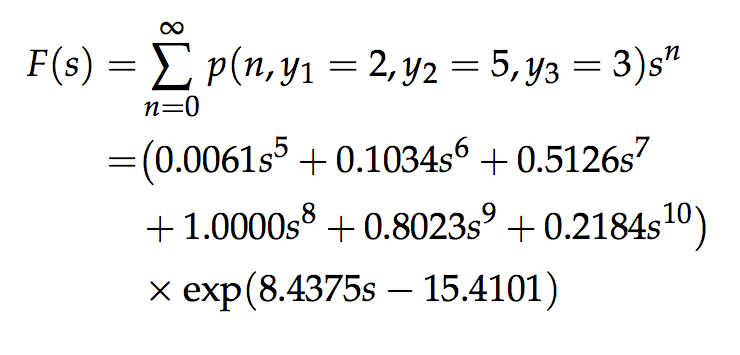
Probabilistic inference is an important tool that allows humans to gain insight and make predictions from data. An analyst posits a probabilistic model for observed data, and then conducts inference to fit parameters, assess model validity, and make predictions. With data growing in size and complexity across nearly all domains of science and society, rich probabilistic models paired with fast and accurate inference algorithms are essential to the data analytic process. Probabilistic graphical models support these goals by leveraging graph structure to design rich models and enable fast message-passing algorithms for inference. However, exact message passing applies only to limited model classes. The goal of this project is to significantly expand the class of models to which message-passing algorithms apply by developing novel representations of probability distributions and messages. The research is expected to significantly improve the available inference techniques for a wide range of models that are encountered in practice, especially in the fields of time-series modeling and population ecology. The project website will be used to disseminate research prototypes.
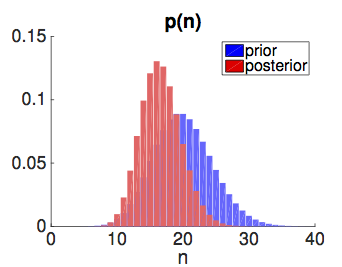
This work proposes two novel representations for factors in graphical models. The first proposed representation is based on probability generating functions for models with count variables. Message passing does not currently apply to these models because the variables have countably infinite support and factors cannot be manipulated in finite space and time using standard representations. However, in many cases, probability generating functions can represent countably infinite factors exactly and compactly. The goal of the proposed work is develop expressive classes of generating functions that are amenable to algorithmic manipulation and can represent commonly appearing factors in graphical models, and then to develop exact and approximate algorithms to perform message passing directly in the space of generating functions. The second proposed representation is based on piecewise-exponential functions, which provide approximate representations of continuous densities. Piecewise-exponential functions are compact, computationally tractable, and provide a tunable level of approximation. They apply to models with continuous but non-Gaussian variables. The goal of the proposed work is to develop techniques to construct accurate piecewise exponential approximations and propagate them within message-passing algorithms. The algorithms developed by this work will be tested and applied to improve inference in existing models and provide new capabilities for models in population ecology.
Probabilistic inference with generating functions for Poisson latent variable models.
K. Winner and D. Sheldon. Proceedings of Neural Information Processing Systems (NIPS), 2016. [pdf].
Exact inference for integer latent-variable models.
K. Winner, D. Sujono, and D. Sheldon. Proceedings of International Conference on Machine Learning (ICML), 2017. [pdf].
Differentially Private Learning of Undirected Graphical Models Using Collective Graphical Models.
G. Bernstein, R. McKenna, T. Sun, D. Sheldon, M. Hay, and G. Miklau. Proceedings of International Conference on Machine Learning (ICML), 2017. [pdf].