Gaze Control for Face
Learning and Recognition by Humans and Machines
John M. Henderson1,4,
Richard Falk1,4, Silviu Minut2, Fred C. Dyer3,4,
and Sridhar Mahadevan2,4
1Department of Psychology
2Department of Computer
Science
3Department of Zoology
4Cognitive Science Program
Draft
of chapter to appear in: T. Shipley and P. Kellman (Eds.), From Fragments to
Objects: Segmentation and Grouping in Vision.
8/26/00
Please
address correspondence to:
John
M. Henderson
129
Psychology Research Building
Michigan
State University
East
Lansing, MI 48824-1117
Email:
john@eyelab.msu.edu
Abstract
In
this chapter we describe an ongoing project designed to investigate gaze
control in face perception, a problem of central importance in both human and
machine vision. The project uses converging evidence from behavioral studies of
human observers and computational studies in machine vision. The research is
guided by a formal framework for understanding gaze control based on Markov
decision processes (MDPs). Behavioral data from human observers provide new
insight into gaze control in a complex task, and are used to motivate an
artificial gaze control system using the Markov approach. Furthermore, the
efficacy of a Markov approach to gaze control for face recognition in machine
vision is tested. The general goal of the project is to uncover key principles
of gaze control that cut across the specific implementation of the system
(biological or machine).
Introduction
The Problem of Gaze Control
The majority of work in human and
machine vision to date has made the simplifying assumption that visual acuity
during stimulus input is equally good across the image to be processed. A
property of human perception, though, is that high acuity vision is restricted
to a small (2º) foveal region surrounding fixation, with acuity dropping off
precipitously from the fixation point (Anstis, 1974; Riggs, 1965). The human
visual system takes advantage of this high-acuity region by rapidly reorienting
the eyes via very fast (saccadic) eye movements (Buswell, 1935; Henderson &
Hollingworth, 1998, 1999; Rayner, 1998; Yarbus, 1967). Recent work in computer
vision and robotics (Kuniyoshi et al., 1995; Brooks et al., 1998) suggests that outfitting
artificial vision systems with a central high-acuity region can similarly
provide important computational advantages in computer vision. However,
foveated vision systems require that the direction of gaze be controlled so
that the foveal region is appropriately directed within the image based on the
properties of the stimulus and the goals of the agent (human or machine), a
complex real-time learning and control problem. The interdisciplinary project
described in this chapter is an attempt to integrate the study of human and
machine gaze control during face learning and recognition, with the ultimate
goal of shedding light on the underlying principles and properties of gaze
control within the important context of face perception.
Gaze Control in Human Vision.
The human visual system takes advantage of the high resolving power of the
fovea by reorienting the fixation point around the viewed scene an average of
three times each second via saccadic eye movements. Saccades are ballistic,
very fast sweeps (velocities of up to 900º/s; Carpenter, 1988) of gaze position
across the scene during which visual information acquisition is severely
limited (Matin, 1974; Volkmann, 1986). Fixations are brief epochs (averaging
about 300 ms; Henderson & Hollingworth, 1998) in which the fovea is
directed at a point of interest, gaze position remains relatively still, and
pattern information is acquired from the scene. Given the importance of
foveation in human vision, the control of fixation placement over time (gaze
control) is a critical sequential decision-making problem. Furthermore, gaze
control appears to have important consequences for other cognitive processes
beyond the timely and efficient acquisition of visual information. For example,
Ballard and colleagues have suggested that fixation is necessary for enabling
computations that require the binding of cognitive and motor processes to
external objects (Ballard, 1996; Ballard et al., in press; also Henderson,
1996; Milner & Goodale, 1995). An important issue in the study of vision
and visual cognition therefore is the nature of the process that controls
sequential decision-making for saccadic eye movements during dynamic visual and
cognitive tasks.
Gaze
Control in Computer Vision. Most classical computer vision methods process
images at constant resolution. In contrast, in human vision the magnitude and
complexity of the input is reduced by a decrease in the resolution of the
visual field from the fovea to the periphery. This decrease in resolution
across the retina leads to loss of information, but the human visual system
compensates for the loss by employing an efficient gaze control mechanism,
directing the fovea to different points in the image to gather more detailed
information as it is needed. Thus, rather than analyzing an enormous amount of
detailed visual information at once, a computationally expensive proposition,
the brain processes detailed information sequentially, turning vision in part
into a sequential decision‑making
process. Only recently has the importance and the potential of foveated
vision been discovered in computer vision, and work in this direction is very
early in development. Currently very few artificial foveated vision systems
exist (Kunioshy 1995, van der Soiegel 1989, Bandera 1996). As these foveated
vision systems develop, algorithms will be required to control the timely
placement of the artificial fovea over the external scene.
A central
component of a successful general theory of gaze control will be an account of
how the perceiving agent– whether it be a human or a machine– can decide where
to fixate at each point in time. This problem of sequential decision‑making
for gaze control is formidable. The
world offers a dizzying array of stimuli to which the agent could direct the
fovea. Compounding the problem, the consequences of particular alternative
actions (foveating Feature A rather than Feature B, C, D... N) may not become
apparent until a sequence of related fixations has been taken, and yet the
perceiving agent may need to estimate the likely payoff of a particular fixation
(or sequence of fixations) in advance. Furthermore, for a perceiving agent,
decisions about fixation position need to be made in quick succession, leaving
little time to sort through the space of all possible fixation placements and
associated outcomes. Finally, a well‑designed agent should be able to
modify its fixation behavior through learning, raising the problem of how to
assign credit to the correct decision and how to store all this information in
memory.
The Problem of Face Perception
Face
Perception in Human Vision. Faces are arguably the most important and salient
visual stimulus a human ever encounters. Faces are central in human social
interaction, providing critical information about the age, gender, emotional
state, intention, and identity of another. There is substantial evidence that
the perception of faces by human observers may be “special” in at least two
ways. First, the computational processes responsible for face perception appear
to be qualitatively different from those involved in the recognition of other
kinds of objects or complex scenes. This view is supported by behavioral data
showing that faces are preferentially attended by young infants when compared
to similarly complex visual stimuli or even scrambled faces (Bruce, 1988). When
placed in complex scenes, faces preferentially draw the attention of adult
viewers (Yarbus, 1967). Inverting a face disrupts face recognition to a greater
degree than does inverting other types of objects (Yin, 1969). Second, the
neural systems that underlie face perception appear to be partially independent
of those systems that underlie object perception more generally. For example,
single cell recording from neurons in the temporal cortex of monkeys has
revealed a population of cells that respond selectively to faces, and in some
cases to specific faces (Desimone, 1991). Evidence from human neuropsychology
has provided examples for a double dissociation between object and face
recognition, with some patients showing intact face recognition and impaired
object recognition (prosopagnosia), and other patients showing the opposite
pattern (visual object agnosia; e.g., Moscovitch et al., 1997; Newcome et al.,
1994). Recent functional neuroimaging studies similarly provide evidence that
face recognition is supported by a neural module in the fusiform gyrus of the
human cortex that is not active during perception of other types of objects
(Ishai et al., 1997; Kanwisher et al., 1997; McCarthy et al., 1997), though it
has been suggested that this area may be more generally devoted to the analysis
of exemplars of a well-learned object class (Diamond & Carey, 1986; Gautier
et al., 1997). Together, these converging sources of evidence strongly support
the hypothesis that the human visual system contains specialized neural and
computational systems that are devoted to face perception. However, the
specific nature of those computations remains very much unresolved.
Face Perception in Computer
Vision. Face recognition is a well-studied problem in computer vision, but
is not completely solved. The problem is typically posed in the following way:
Suppose we have a database of images of N people. In general, all images are the same size,
and there are several images for each person. Given a test image (i.e., an image
of a person whose identity is not known), one must detect whether or not the
person is in the database, and if it is, correctly identify that person. The
traditional approach is to treat each image as a (high dimensional) vector by
concatenating the rows of pixels that compose it (e.g. see Pentland et al., 1994). The
dimensionality of the vector, K, equals the total number of pixels in
the image; each dimension is a measure of the gray-scale level (or color) of a
particular pixel in the image. Analyzed in this way, each image in the database
defines a point in a K-dimensional Euclidean space. If it turns out that
images of the same person are closer to each other in this space than they are
close to images of other people, a clustering algorithm can be used to form
decision boundaries. Thus, to classify a test image it suffices to determine
the class of its nearest neighbors or, in other words, to determine the cluster
to which that image belongs. Although appealing, this basic scheme is difficult
to implement, for reasons of dimension. An image as small as 60 x 80 pixels
yields a vector of dimension 4800. If the database contains a few hundred
images, it is difficult if not impossible to find the nearest neighbors in
reasonable time.
A considerable number of techniques
that try to reduce the dimensionality of the problem are known, each with its own
strengths and weaknesses. These include Principal Component Analysis (Pentland
et al., 1994), Neural Networks (Mitchell, 1997) and Markov models (Samaria et
al., 1994). From a purely computational point of view, any method is
acceptable, as long as it produces high classification rates, e.g., see recent
work on probabilistic face matching (Mogaddam et al., 1998). Such methods do
not have to imitate nature. However, there must be a good reason nature chose,
through evolution, certain algorithms over others. From a theoretical point of
view, it is of interest to discover the nature of the algorithms used by the
human brain, and to come to understand why those algorithms have been selected.
Furthermore, the superiority of the algorithms used by the human visual system
(whatever they may be) over standard face recognition (and more generally,
computer vision) algorithms is obvious. Of the frameworks used to reduce the
dimensionality of the face recognition problem, the one that appears most
promising in uncovering the algorithm used by nature, given the characteristics
of the human foveal vision system, is a sequential decision-making framework.
Our work thus asks the following fundamental question: How important is foveal
vision in face recognition?
An Investigation of Gaze
Control in Face Learning and Recognition
We have recently undertaken an
initial investigation designed to integrate the study of gaze control for face
learning and recognition across humans and artificial agents. This
investigation entailed a behavioral study of gaze control with human
participants, and the implementation of a face learning and recognition system
within a Hidden Markov Model (HMM) framework. In this section we will summarize
the work so far and the promise it holds for the future.
Behavioral Study:
Human Gaze Control during Face Learning and Recognition
In an initial behavioral study
(Falk, Hollingworth, Henderson, Mahadevan, & Dyer, 2000), we asked 16
participants to view full-color images of human faces in two phases, a study
phase in which the participants were asked to learn the faces of twenty
previously unknown undergraduate women, and a recognition phase in which the participants
were asked to distinguish these learned faces from distracter faces, drawn from
the same pool, that had not been learned. In addition, during the recognition
phase, half of the previously learned and half of the new (distracter) faces
were presented upright, and half were presented upside-down. The purpose of
this latter manipulation was to examine whether differences in gaze control to
upright and inverted faces might be related to fixation position or scanning
sequence.
The method of the experiment was as
follows: In the Study Phase, 16 participants viewed a series of 20 upright
faces for 10 sec each, with the order of faces and conditions randomized within
the block. The participants then viewed a series of 10 pictures of naturalistic
scenes for 10 sec each, with the order of scenes randomized within the block.
This scene viewing phase constituted a period of time over which the learned
faces had to be remembered. In the Recognition Phase, the same 16 participants
viewed 10 new upright faces, 10 new inverted faces, 10 previously learned
upright faces, and 10 previously learned inverted faces. Each face was
presented until the participant responded, or for 20 sec maximum. All four
types of face stimuli were presented in a single block, with order of stimuli
(and hence condition) randomized within that block. Assignment of particular
faces to particular learning and recognition conditions (learned or distracter,
upright or inverted) was counterbalanced over participants.
The face stimuli used in the study were generated
from photographs of undergraduate women with dark hair. The photographs were
scanned into a computer and cropped so that each picture included only the face
and hair. Hair was also cropped so that its style was relatively uniform across
the set of stimuli (See Figure 1 for an example). Faces that included
distinctive features such as eyeglasses, jewelry, moles, and so on were not
used. Each cropped face was pasted onto a uniform gray background. All images
were presented at a resolution of 800 by 600 pixels by 15 bit color (32,768
colors) and appeared photographic in quality. The faces subtended 7.56º
horizontally by 10.47º vertically on average at a distance of about 1 meter;
thus, they appeared at a natural size for a human face at this viewing
distance.
 The viewer's eye position over the course of face
learning and recognition was precisely tracked using a Generation 5.5 Stanford
Research Institute Dual Purkinje Image Eyetracker (Crane, 1994; Crane &
Steele, 1985). Eye position was sampled at 1000 Hz, with spatial resolution
better than 10' of arc.
The viewer's eye position over the course of face
learning and recognition was precisely tracked using a Generation 5.5 Stanford
Research Institute Dual Purkinje Image Eyetracker (Crane, 1994; Crane &
Steele, 1985). Eye position was sampled at 1000 Hz, with spatial resolution
better than 10' of arc.


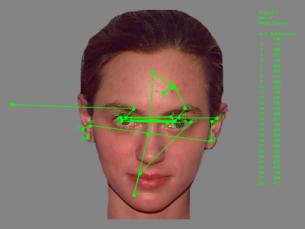 Summary of Results. Study Phase. Figure
1 presents the scan pattern (the sequence of fixations and saccades) of a
single participant viewing a single face during the study phase. The straight
lines represent saccades, and the dots represent fixations. This scan pattern
is typical: Participants tended to focus on the salient features of the faces,
including the eyes, the nose, the mouth.
Summary of Results. Study Phase. Figure
1 presents the scan pattern (the sequence of fixations and saccades) of a
single participant viewing a single face during the study phase. The straight
lines represent saccades, and the dots represent fixations. This scan pattern
is typical: Participants tended to focus on the salient features of the faces,
including the eyes, the nose, the mouth.
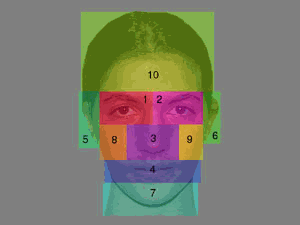
To
quantitatively examine the data, each face was divided into ten scoring
regions, consisting of the two eyes, the nose, the mouth, the two ears, the
chin, the two cheeks, and the forehead, as shown in Figure 2. All fixations for
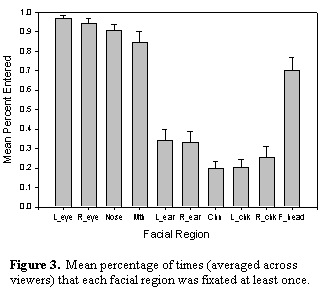
each participant were then assigned to one of these regions. Figure 3 shows the mean
percentage of times each facial region was entered at least once during a
trial. As can be seen, both eyes were fixated at least once in over 95% of all
trials. The nose, mouth, and forehead were also examined with a high degree of
regularity, whereas the cheeks, ears, and chin were rarely fixated over the
course of 10 seconds of viewing time. Thus, consistent
with the qualitative results of prior face viewing studies, participants
generally distributed the majority of their fixations on or near important
facial features (e.g., Buswell, 1935; Yarbus, 1967).
|
|
Target
Region
|
||||||||||
|
Source
Region |
Region
|
L_Eye |
R_Eye |
Nose |
Mouth |
L_Ear |
R_Ear |
Chin |
L_Chk |
R_Chk |
F_Head |
|
L_Eye |
+ |
+ |
|
|
|
- |
- |
|
- |
|
|
|
R_Eye |
|
+ |
- |
|
- |
|
- |
- |
|
|
|
|
Nose |
|
- |
+ |
+ |
|
- |
|
|
|
- |
|
|
Mouth |
|
- |
|
|
|
|
+ |
|
|
- |
|
|
L_Ear |
|
- |
- |
|
+ |
|
|
|
|
|
|
|
R_Ear |
- |
|
- |
|
|
+ |
|
|
|
|
|
|
Chin |
- |
- |
|
|
|
|
+ |
|
|
- |
|
|
L_Chk |
|
- |
|
|
|
|
|
|
|
|
|
|
R_Chk |
- |
|
|
|
|
|
|
|
|
- |
|
|
F_Head |
- |
|
- |
- |
|
|
|
|
|
+ |
|
|
Table 1. Deviations of fixation transition frequencies observed in the first-order Markov matrix from the frequencies predicted by the zero-order Markov matrix. Positive (+) indicates more observed fixations than predicted. Negative (-) indicates fewer observed fixations than predicted. |
|||||||||||
Fixation sequences (an example of which is shown in
the figure above) were analyzed using zero- and first-order Markov transition
matrices of fixation sequences from the pre-defined face regions shown in
Figure 2. A
Markov analysis quantitatively characterizes the distribution of gaze
transitions from one fixation position to the next. The goal of the Markov
analysis was to determine if the location of fixation position n, and
hence perceptual and cognitive processing during fixation n, influences
the spatial placement of fixation n+1. The zero-order matrix captures the
probability of fixating a given region (zero-order Markov matrix), and the
first-order Markov matrix captures the probability of moving to a given region
from another given region. If the location of the current fixation does significantly influence
where subsequent fixations are made, then the first-order matrix should deviate
from that predicted by the base probabilities represented by the zero-order
matrix. The method used for computing the zero- and first order matrices was
modified from that given by Liu (1998).
Table 1 provides a summary of the Markov matrix
analysis. Chi-squared
tests of deviations of observed fixation positions from those that would be
expected based on the marginal (zero-order) matrices showed systematic
deviations from base probabilities, suggesting that there was a degree of
regularity in the fixation sequences. A non-zero number in the difference matrix in Table
1 indicates a reliable difference between the predicted first-order matrix and
the observed first-order matrix as determined by the Chi-Square analysis. A
plus sign in the difference matrix means that there were more observed
transitions in that cell than would be predicted from the zero-order matrix. A
minus sign indicates fewer transitions than would be predicted. As Table 1
demonstrates, in several instances position of fixation n significantly
affected the selection of fixation n+1 position. For example, notice
that along the diagonal axis there is almost a uniform influence of current
fixation position. This shows that the tendency to refixate the currently
fixated facial region was higher than that predicted by baseline fixation
rates. Second, there were a large number or transitions from one eye to the
other, suggesting a greater likelihood of moving to an eye if the other eye was
presently fixated. These data provide additional evidence that the eyes are a
particularly important or salient facial features for gaze targeting during
face learning.
Recognition Phase. In the
Recognition Phase, participants viewed the twenty previously learned faces and
20 new faces drawn from the same pool. Half of the new and old faces were
presented upright, and half were presented upside-down. Participants viewed
each face freely and indicated, via button press, whether the current face was
new or was one of the faces viewed during the learning phase. When the
participant pressed the response button, the current face was removed from the
computer screen and, following a brief calibration screen, the next face was
displayed.
Overall accuracy in the Recognition Phase, collapsed
over new and old faces, was about 73% correct. As expected from the face
recognition literature, accuracy was influenced by the orientation of the face
in the Recognition Phase, with accuracy of about 79% in the upright condition
and 66% in the inverted condition. Average viewing time during the Recognition
Phase was about 2.3 seconds, with participants taking about 560 ms longer to
respond to new than to learned faces, and about 144 ms longer to respond to
inverted than to upright faces.

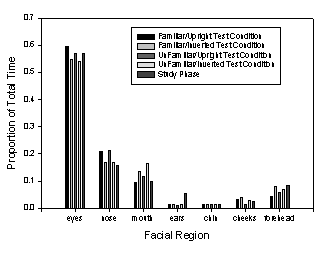 Interestingly, although viewing time in the Recognition
Phase was about an order of magnitude shorter than in the Learning Phase, the
distribution of fixations over the faces in these two phases was remarkably
similar (Falk, Hollingworth, Henderson, Mahadevan, & Dyer, 2000). This
similarity can be seen in Figure 4, which shows the proportion of total time
spent on the major features defined in Figure 2. As can be seen, the same
features received the same proportion of total fixation time in the Learning
and Recognition Phases. Also clear in Figure 4 is the fact that inversion in
the Recognition Phase had little influence on the distribution of fixation time
over the faces. A similar pattern is observed when proportion of discrete
fixations rather than proportion of fixation time is used as the dependent
measure. These data suggest that, at least insofar as the overt selection of
facial features for visual analysis is concerned, the face inversion effect is
not due to a transition from more wholistic face processing to more local,
feature-based processing.
Interestingly, although viewing time in the Recognition
Phase was about an order of magnitude shorter than in the Learning Phase, the
distribution of fixations over the faces in these two phases was remarkably
similar (Falk, Hollingworth, Henderson, Mahadevan, & Dyer, 2000). This
similarity can be seen in Figure 4, which shows the proportion of total time
spent on the major features defined in Figure 2. As can be seen, the same
features received the same proportion of total fixation time in the Learning
and Recognition Phases. Also clear in Figure 4 is the fact that inversion in
the Recognition Phase had little influence on the distribution of fixation time
over the faces. A similar pattern is observed when proportion of discrete
fixations rather than proportion of fixation time is used as the dependent
measure. These data suggest that, at least insofar as the overt selection of
facial features for visual analysis is concerned, the face inversion effect is
not due to a transition from more wholistic face processing to more local,
feature-based processing.
We can draw four main conclusions
from this behavioral study. First, selection of facial features through overt
orienting of the eyes is observed during both face learning and recognition.
Although we don't have evidence here that gaze control is strictly necessary
for face learning and recognition, it is striking that when allowed to view
faces freely, human observers moved their eyes over the face, making clear
choices about which features to orient to and which to ignore. Second, as shown
by the results of the Markov analysis, the selection of a fixation site during
learning is driven, in part, by the specific feature that is currently under
fixation. Thus, there is some sequential dependency to gaze control decisions.
Third, the facial features selected for fixation during recognition are very
similar to those selected for fixation during learning. It is tempting to
conclude that feature processing during learning influences this selection
during recognition, though we do not yet have direct evidence for this
proposition. Fourth, the facial features selected for fixation during
recognition of an upright face are very similar to those selected for fixation
during recognition of an inverted face. This finding is intriguing, because one
might have expected that recognition of upright faces, hypothesized to be
supported by wholistic pattern processing, would lead to less feature-specific
analysis than would inverted faces, which are hypothesized to be supported by
feature-based analysis (Farah, Tanaka, & Drain, 1995; Tanaka & Farah, 1993).
Formal
Framework: A Probabilistic Model of Sequential Decision Making
We have seen in the previous section
that human gaze control is regular and efficient. It is deeply puzzling how to
endow machines with the apparent fluidity and accuracy of human gaze control.
What is needed is a formal framework that both accounts for patterns of human
gaze and allows the development of algorithms for gaze control of an artificial
visual system. The long-term goal of our project is to investigate whether
Markov decision processes (MDPs) can be the basis of such a framework.
MDPs are a well-developed formal framework for
studying sequential decision making, originally proposed in the operations
research literature (Bellman, 1957; Howard, 1960; Puterman, 1994). In recent
years, MDPs have become a unifying formalism for studying a range of problems
in artificial intelligence and robotics, from planning in uncertain
environments (Kaelbling, 1998) to learning from delayed reward (Mahadevan et
al., 1992). The MDP framework comprises a range of different models, from the
simple case of Markov chains when states are observable and there is no
choice of action, to the intermediate cases of hidden-Markov models
(HMMs) when states are not observable but there is no action choice and Markov
decision processes (MDPs) where states are observable but there is a choice
of action, leading finally up to the most complex case of partially-observable
MDPs (POMDPs) where states are not observable and the agent has a choice of
action in any state. In our project to date, we have focused first on the HMM
case, since the underlying states during the process of face recognition are
not themselves observable, but have to be inferred from fixation points during
recognition. Our goal is to use the simpler HMM case as a jumping-off point to
the more complex POMDP problem of allowing the agent choice of what the next
fixation point should be. One advantage of starting with the HMM case is that
the principal algorithms for learning an HMM model (the well-known Baum Welch,
forward-backward, and Viterbi algorithms) all extend nicely to the POMDP case.
Computational
Study: Gaze Control for Face Recognition using Hidden Markov Models
In a recent study we tested the potential of the HMM
formalism in face recognition (Minut, Mahadevan, Henderson, & Dyer, 2000).
HMMs are in one important respect not a good model of human gaze control, since
humans clearly do not follow a fixed, predetermined sequence of action when
scanning faces. However, HMMs are
appealing because they do not require us to specify the nature of the
underlying states of the system (which are not known for human gaze control),
only the actions available to it (shifts of gaze), and the (probabilistic) effects of the actions on
the information available to the system.
Furthermore, it should eventually be possible to build on the HMM
framework to introduce more flexible selection of action, hence turning it into
a POMDP.
We used a database consisting of 27
women and 19 men with 6 images per person, as shown in Figure 5.






Figure 5. Face stimuli used in the HMM study.
Each
image was 512x512 pixels. We defined 10 regions of interest for each face,
loosely based on the human fixation patterns we observed in the behavioral
study, and we built a left to right HMM corresponding to these regions (see
Figure 6).

 The goal of this experiment was to build an HMM for each
class (person) in the database, using input from a foveated vision system. To
this end we produced for each image an observation sequence that consisted of
30 observation vectors. Each observation vector was produced by foveating on
the same image multiple times. The system fixated 3 times in each of the 10
regions, and moved to the next region in sequence. This order was of course
arbitrarily imposed by us and does not agree with the patterns that human
subjects seem to follow. The HMM was built when all of its parameters had been
learned (i.e. all the state transition probabilities and all the observation
density functions). The parameters were learned (updated) incrementally, as new
observation sequences were processed. The HMMs for different classes had the
same states, but different parameters. Each HMM was built based on 5 images for
each class, with the 6th image used for testing of recognition performance.
Thus, recognition was tested using images that had not been seen during
learning.
The goal of this experiment was to build an HMM for each
class (person) in the database, using input from a foveated vision system. To
this end we produced for each image an observation sequence that consisted of
30 observation vectors. Each observation vector was produced by foveating on
the same image multiple times. The system fixated 3 times in each of the 10
regions, and moved to the next region in sequence. This order was of course
arbitrarily imposed by us and does not agree with the patterns that human
subjects seem to follow. The HMM was built when all of its parameters had been
learned (i.e. all the state transition probabilities and all the observation
density functions). The parameters were learned (updated) incrementally, as new
observation sequences were processed. The HMMs for different classes had the
same states, but different parameters. Each HMM was built based on 5 images for
each class, with the 6th image used for testing of recognition performance.
Thus, recognition was tested using images that had not been seen during
learning.
 In this study, our simulated fovea was a software-defined
square patch centered at the desired fixation point, of the same resolution as
the original unfoveated image. We surround this patch with rings of
“superpixels'” which double in size as we move from the center towards the
periphery of the image. A superpixel is simply a small square patch whose size
is a few (physical) pixels. All pixels that make up a superpixel have the same
graylevel value, namely the average of the pixels in the same region in the
original image. Within a ring, all superpixels have the same size. Their size
doubles only when one moves from one ring to another. Furthermore, each ring
contains the same number of layers of superpixels. (Figure 7 shows a 512 x 512
image (1:4 scale), fixation on the left eye.). A second dimensionality reduction
is then achieved by applying a standard compression technique (DCT) to the
image (Figure 8 shows the reduced image obtained by mapping each superpixel to
a single physical pixel).
In this study, our simulated fovea was a software-defined
square patch centered at the desired fixation point, of the same resolution as
the original unfoveated image. We surround this patch with rings of
“superpixels'” which double in size as we move from the center towards the
periphery of the image. A superpixel is simply a small square patch whose size
is a few (physical) pixels. All pixels that make up a superpixel have the same
graylevel value, namely the average of the pixels in the same region in the
original image. Within a ring, all superpixels have the same size. Their size
doubles only when one moves from one ring to another. Furthermore, each ring
contains the same number of layers of superpixels. (Figure 7 shows a 512 x 512
image (1:4 scale), fixation on the left eye.). A second dimensionality reduction
is then achieved by applying a standard compression technique (DCT) to the
image (Figure 8 shows the reduced image obtained by mapping each superpixel to
a single physical pixel).
 HMMs have been used recently to model faces ( Nefian
& Hayes, 1999; Samaria & Young, 1994). However, those implementations
did not make use of foveated vision. Instead, the observations for each image
were produced by first dividing the image into horizontal (overlapping)
stripes, and then computing the DCT coefficients in each stripe. The images
used were already small (about 100 x 100 pixels), 25 times smaller than our
images. Any attempt to run the HMM algorithms using observations coming from
512 x 512 images would be futile. In order to compare our method with Samaria's
we had to reduce the size of our images through subsampling (vs foveation) in
order to achieve constant resolution.
HMMs have been used recently to model faces ( Nefian
& Hayes, 1999; Samaria & Young, 1994). However, those implementations
did not make use of foveated vision. Instead, the observations for each image
were produced by first dividing the image into horizontal (overlapping)
stripes, and then computing the DCT coefficients in each stripe. The images
used were already small (about 100 x 100 pixels), 25 times smaller than our
images. Any attempt to run the HMM algorithms using observations coming from
512 x 512 images would be futile. In order to compare our method with Samaria's
we had to reduce the size of our images through subsampling (vs foveation) in
order to achieve constant resolution.
In this study ten regions of each
face were foveated (three fixations in each region), and we varied the number
of states in the HMMs from 3 to 10, comparing foveated vision and subsampling.
Interestingly, peak performance for foveated vision was observed at about 6‑7
states, rather than 10, as expected (see Figure 9). Since the fixation points
are spread rather uniformly in the ten regions across the image, it is unlikely
that the states arose due to clustering, and it is very intriguing why the HMM
algorithms, purely mathematical in nature, came up with an optimum of 6‑7
states. This may suggest that the states of the recognition process do not
correspond to regions in the image. It is also interesting to note that the optimal
number of states for subsampling is different (and higher) than the optimal
number of states for the HMMs built through foveation

 Although our purpose was not necessarily to produce a
better recognizer, but rather to determine if the HMM framework using foveated
vision could produce at
least reasonable results, it is interesting that we achieved higher accuracy
using foveation than with subsampling (see Figure 9). In addition, the
sequential decision-making framework represented by the HMM approach has other
advantages. For example, it provides a method that allows incremental learning
of new classes. That is, new faces can be added to the database without
recomputing the representations of all other learned faces. We are encouraged
that performance benefits may be derived from incorporating foveal vision and
sequential information acquisition into artificial recognition systems.
Although our purpose was not necessarily to produce a
better recognizer, but rather to determine if the HMM framework using foveated
vision could produce at
least reasonable results, it is interesting that we achieved higher accuracy
using foveation than with subsampling (see Figure 9). In addition, the
sequential decision-making framework represented by the HMM approach has other
advantages. For example, it provides a method that allows incremental learning
of new classes. That is, new faces can be added to the database without
recomputing the representations of all other learned faces. We are encouraged
that performance benefits may be derived from incorporating foveal vision and
sequential information acquisition into artificial recognition systems.
The MDP Approach to Gaze Control
for Face Perception. The MDP approach to decision making provides an
exciting framework within which to study human gaze control for face
perception. These models provide a formalism that can be used to generate
specific hypotheses about the decision processes supporting gaze control.
Importantly, these models can be formulated at the appropriate temporal and
spatial grain size, with an action conceptualized as a “macro” that specifies the goal of the saccadic
system in a hierarchical control structure. Conceptualizing gaze control at
this grain size is consistent with current cortical control models
(Pierrot-Deseilligny et al., 1995), and makes the decision process far more
tractable (Precup et al., 1997). In addition, recent work on foveated vision
and gaze control in AI and robotics suggests that the MDP approach may provide
new insights into decision-making for fixation placement and the manner in
which gaze control is learned and optimized to support new perceptual tasks
(Bandera et al., 1996; Darrell, 1995; Rimey & Brown, 1991).
Although there has been some work on
the applicability of Markov models to human scan patterns, this work has
predominantly been descriptive and motivated by a theory of perceptual memory
(the scan path theory, Noton & Stark, 1971) that has not been strongly
supported by the behavioral data (Groner et al., 1984; Stark & Ellis,
1981). Furthermore, little work has specifically attempted to integrate Markov
analyses of gaze control with face perception and recognition (though see Althoff
& Cohen, 1999). Finally, prior work applying Markov models to human gaze
control has focused on the sequence of fixation placement. Another important
aspect of gaze control is the duration of each fixation. Fixation durations in
scene viewing have a mean of about 300 ms, but there is considerable
variability around this mean (Henderson & Hollingworth, 1998). A
substantial proportion of this variability is accounted for by the fact that an
important function of gaze control is to gain information about the world, as
suggested by the findings that fixation durations are shorter for semantically
constrained objects (Friedman, 1979; Henderson et al., 1999; Loftus &
Mackworth, 1978) and objects that have been fixated previously (Friedman,
1979).
Human eye movements are examples of actions whose
primary purpose is to gain information, not to change the state of the world.
Such information-gathering actions naturally arise in partially observable
environments, where the agent does not have complete knowledge of the
underlying state. POMDPs are an approach to extending the MDP model to modeling
incomplete perceptions, as well as to naturally treat actions that change the
state as well as collect information (Kaelbling et al., 1998). Here, in
addition to states and actions, there is a finite set of observations O
(much smaller than the set of states), where an individual observation may be a
stochastic function of the underlying state. POMDPs can be viewed as MDPs over
a much larger set of belief states, which are a vector of estimates of the
probability that the agent is in each of the underlying real states. Given a
belief state, the agent can update the belief state on the basis of new
observations and actions in a purely local manner. However, finding optimal policies
in a known POMDP model is intractable, even for problems with as few as 30
states (Littman, 1996). The ultimate goal of our work is to determine how
humans are able to solve POMDPs in restricted situations, such as face
recognition, by exploiting particular properties of the image (e.g. faces are
symmetric, and the main features of a face remain invariant over age or
ethnicity). We assume that careful investigations of human gaze control will
provide insights into how artificial gaze control systems can meet these
challenges. These insights will not only lead to a better theoretical
understanding of gaze control in humans and machines, but also result in
practical algorithms for robots.
Conclusion
The
ability to control the direction of gaze in order to properly orient the fovea
to important regions of the external world is important for all mammals,
including humans. This ability is especially critical in the case of face
perception, where the need to quickly determine the identity, kinship, intention,
and emotional state of another is central to all social interaction and
presumably, to survival. In human vision, evidence suggests that the ability to
learn and recognize faces uses dedicated neural and cognitive systems that have
evolved to support it. In machine vision, face perception is an important
test-bed for computational theories of vision, is necessary for constructing
robotic systems that can interact socially with humans, and has important
practical applications in the construction of computer security systems that
operate via person identification. The promise of foveated vision systems with
appropriate gaze control for artificial vision is in its infancy, but holds
great promise.
Our
current work is designed to extend our study of gaze control during face
learning and recognition. We are particularly interested in finding answers to
three specific questions: First, how are potential fixation targets selected by
human observers, what stimulus factors determine which target is fixated next,
and what advantages are conferred by choosing these fixation sites over others?
Second, to what degree is the specific ordinal sequence of fixations important
in the perceptual learning and recognition of faces? Third, to what degree is
the ordinal fixation sequence over faces affected by factors such as the
viewing task and the stimulus set? We are addressing these questions by using
converging methods from behavioral studies of human gaze control and MDP
studies using computational modeling and implementation of artificial gaze
control.