Descriptive Complexity

Computational complexity was originally defined in terms of the natural entities of time and space, and the term complexity was used to denote the time or space used in the computation. Rather than checking whether an input satisfies a property S, a more natural question might be, what is the complexity of expressing the property S? These two issues -- checking and expressing -- are closely related. It is startling how closely tied they are when the latter refers to expressing the property in first-order logic of finite and ordered structures. In 1974 Fagin gave a characterization of nondeterministic polynomial time as the set of properties expressible in second-order existential logic. Extending this theorem, our research has related first-order expressibility to computational complexity. Some of the results arising from this approach include characterizing polynomial time as the set of properties expressible in first-order logic plus a least fixed-point operator, and showing that parallel time on a Parallel Random Access Machine is linearly related to first-order inductive depth. This research has settled a major, long standing question in complexity theory by proving the following result: For all s(n) greater than or equal to log n, nondeterministic space s(n) is closed under complementation.

See Neil Immerman's Recent Publications, for some publications on descriptive complexity, and "Recent Talks", for video and slides of a recent survey talk on Descriptive Complexity.

Natural complexity classes tend to have natural descriptive characterizations. For example, here is a diagram of the world of computability and complexity:

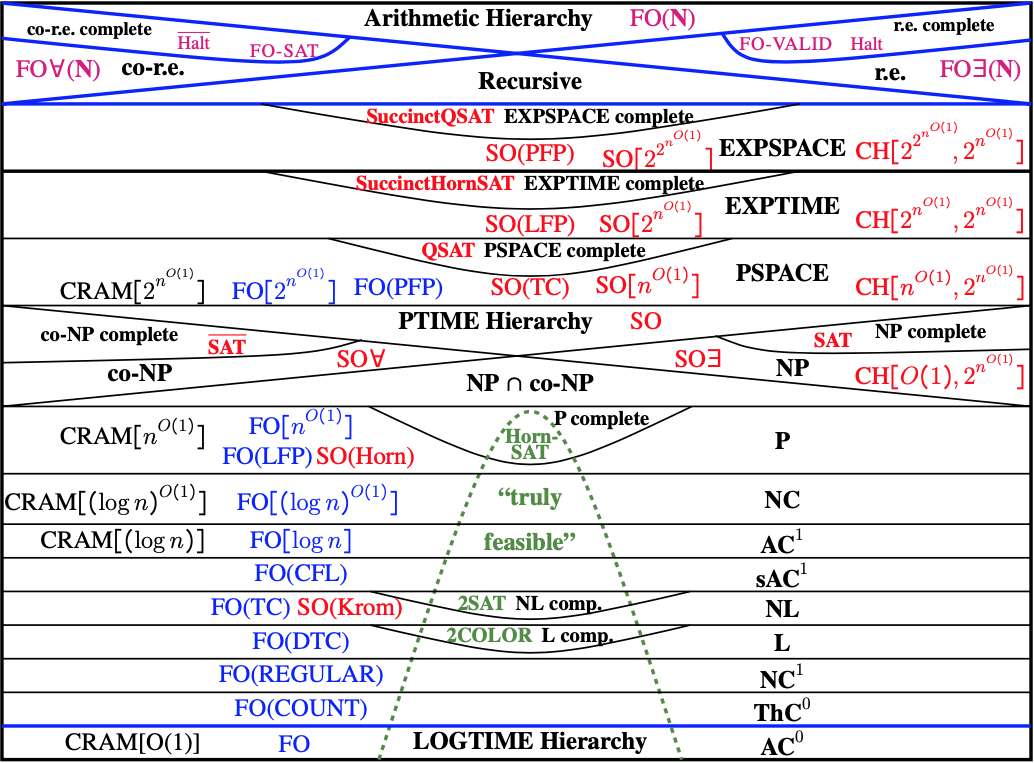
In the above diagram, CRAM[t(n)] is parallel time O(t(n)) on a Concurrent-Read, Concurrent-Write Parallel Random Access Machine, using polynomially much hardware. This is equal to FO[t(n)], the set of problems expressible by a fixed block of first-order restricted quantifiers, recopied t(n) times for structures of size n. CH[t(n),h(n)] is parallel time O(t(n)) on a CRAM using O(h(n)) hardware gates.

The following are descriptive characterizations of some of the above classes. We think of all complexity theoretic problems as sets of finite structures of some vocabulary. Such a problem can be thought of as a boolean-valued query on relational databases. The following characterizations assume that there is a given total ordering on each input structure.

For constructive t(n), FO[t(n)] = IND[t(n)] = CRAM[t(n)].
This means that the boolean queries computable in parallel-time t(n) are exactly those expressible by formulas consisting of a fixed quantifier block, iterated t(n) times, and this is the same as the set of boolean queries expressible via first-order inductive definitions that close in t(n) steps. CRAM[t(n)] means parallel time t(n) on a concurrent read and concurrent write paralllel random access machine that has at most a polynomial amount of memory and processors.
For k = 1, 2, . . ., VAR[k+1] = DSPACE[n^k].
The boolean queries computable using deterministic space n to the power k are exactly those expressible via a block of quantifiers that may be iterated exponentially many times --- as a function of the size of the input structure --- but use only k+1 domain variables.
The Logarithmic-Time Hierarchy = FO = AC⁰ = CRAM[1].
In the lowest level of our chart, the logarithmic-time hierarcy is equal to the set of first-order expressible boolean queries. It is also equal to the set of boolean queries accepted by a uniform sequence of bounded-depth, unbounded fan-in, polynomial-size circuits and to those computable in constant parallel time.
DSPACE[log n] = FO(DTC).
Deterministic Logspace is equal to the set of boolean queries expressible in first-order logic, extended by a deterministic transitive closure operator. Yuri Gurevich gave an alternate characterization of logspace as the set of boolean queries computable by the "finite, primitive-recursive" functions.
NSPACE[log n] = FO(TC) = SO-Krom.
Nondeterministic Logspace is equal to the set of boolean queries expressible in first-order logic, extended by a transitive closure operator. This is also equal to the set of second-order boolean queries in which the first-order part is a universal formula in "Krom" form, i.e., conjunctive normal form with at most two literals per clause. This later characterization is due to Erich Grädel.
For any formula, ϕ(x₁,. . .,x_k, y₁, . . .,y_k), TC(ϕ) denotes the reflexive, transitive closure of the binary relation ϕ. DTC(ϕ) is equal to TC(ϕ_d) where ϕ_d is the deterministic reduct of ϕ,
ϕ_d(x,y) <=> ϕ(x,y) & (∀ z)(ϕ(x,z) -> z = y)
P = FO(LFP) = FO[n^O(1)] = SO-Horn.
Polynomial Time is the set of boolean queries expressible in first-order logic extended by the ability to define new relations by induction. This is formalized via a Least Fixed Point operator. This is sometimes called the Immerman- Vardi Theorem. P is also equal to the set of boolean queries expressible by a quantifier block iterated polynomially many times. Finally, P is equal to second-order boolean queries in which the first-order part is a universal formula in "Horn" form, i.e., conjunctive normal form with at most one positive literal per clause. This later characterization is due to Grädel.
NP = SOE.
Nondeterministic Polynomial Time is equal to the set of boolean queries expressible in second-order, existential logic. This is Fagin's Theorem
PH = SO.
The Polynomial-Time Hierarchy is equal to the set of boolean queries expressible in second-order logic.
PSPACE = FO(PFP) = FO[2^{n^O(1)}] = SO(TC) = SO[n^O(1)]= CH[n^O(1), 2^{n^O(1)}].
Polynomial Space is the set of booean queries expressible by first-order quantifier blocks iterated as much as is useful, i.e., exponentially. This is captured by the power of a Partial Fixed Point Operator. PSPACE can also be charcterized by second-order formulas iterated polynomially many times. A transitive closure operator added to second-order logic captures this.
For constructible t(n), SO[t(n)] = CH[t(n), 2^{n^O(1)}].
Second-Order quantifier blocks iterated t(n) steps times describe the boolean queries computable in parallel time t(n) using exponentially much hardware: "CH[t(n), h(n)]" stands for simultaneous CRAM time O(t(n)) using O(h(n)) hardware gates. Thus, the polynomial-time hierarchy contains those boolean queries computable in constant time using exponentially much hardware. PSPACE is the set of queries computable in polynomial time using exponentially much hardware.
EXPTIME = SO(LFP) = SO[2^{n^O(1)}].
Exponential time is the set of boolean queries computable in second-order logic extended with the capacity to define new relations by induction. This is the same as second-order quantifier blocks that may be iterated exponentially.
The Arithmetic Hierarchy is equal to the set of those sets of natural numbers that are expressible in the first-order theory of N. In all the above characterizations, structures are assumed to be finite and their universes have a total ordering. This last equality is different, but included as a descriptive characterization of the top class in our diagram, and a characterization that is quite analogous to the others.

Descriptive Complexity is part of Finite Model Theory, a branch of Logic and Computer Science.

Thanks to NSF grants CCR-8105754, Mathematical Sciences Postdoctoral Research Fellowship 8311679, CCR-8603346, CCR-8806308, CCR-8996280, CCR-9008416, CCR-9207797, CR-9505446, CCR-9877078, CCF-0207373, CCF-0514621, CCF-0830174, CCF-1115448, CCF-1617498 which helped to support some of the research described on this page.