All comments and corrections are greatly appreciated!
Corrections, Annotations, Additions:
- p 1, l -10:
- "will follow database terminology" should
be "we will follow database terminology".
- p 8:
- In the discussion of operator precedence, "not",
"forall", and "exists" share highest precedence. Also, I hadn't thought much about
operator precedence. I should have said that implication associates from right to
left, so that "a
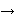 b
b 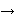 c" is equivalent to
"a
c" is equivalent to
"a 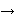 (b
(b 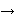 c)"
c)"
- p 8:
- In Example 1.4, the first formula should have been,
ϕundir = (∀ x)(∀ y)(¬ E(x,x) & ( E(x,y) → E(y,x))),
i.e., a reader pointed out that we need the extra parentheses because of
the way we defined operator precedence earlier on the same page!
- p 16:
- In the proof that BIT is first-order expressible using
PLUS and TIMES, the coding is unclear. In addition to the guessed
variables Y and I, one should also guess the variable Z to encode the
position of the last bit of each exponent. For example, the Z of Table
1.19 would have "1"s in positions 12, 5, and 2.
- p 17, l -1:
- "I(A)" should be
"Ib(A)".
- p 20, Exercise 1.29, Part 2:
- "3-ary" should be "2-ary",
i.e., binary. A surprisingly simple modification works!
- p 29, Example 2.12:
- Note that the given reduction is really to bit n-1 of the lower order half
of the 2(n2) bit result of MULT.
- p 31, Exercise 2.16:
- Last line should end "MULTb".
- p 31, l -4:
- "Mb#w#r" should be "MB#w#r".
- p 37, Exercise 2.28:
- By ``linear time'' we mean time
O(n+m) on a random-access machine (RAM). We assume that the edges
of the input circuit are given as an adjacency list; m is the number of
edges.
- p 48, Exercise 3.7:
- In this problem I suggest that you
use Proviso 1.15, i.e., there are two constants 0 and 1 in the
language that are guaranteed to be distinct. Without this, the
exercise is still doable but perhaps a bit too involved.
- p 49, line -10:
- "It follows from Proposition 3.10" should be
"It follows from Proposition 3.5".
- p 49, line -6:
- "IAB(phiB)" should be:
"\widehat{IAB}(phiB)".
- p 55, line 3:
- "Mahaney REACHd showed" should be
"Mahaney showed".
- p 55, line -7:
- At the end of that paragraph, please
add, "Reingold proved in [Rei05] the breakthrough result that REACHu is in L, and thus
that symmetric logspace is equal to L."
- p 62, line -7:
- ``$\times$'' should be ``TIMES''.
- p 62, line -5:
- ``IND[0]'' should be ``IND[1]''.
- p 63, line 2:
- ``MULT'' should be ``TIMES''.
- p 87, line -10:
- The definition of ACCEPTM(ID1) is missing the
following third
conjunct: (ID1 is universal → (∀
ID2)(APATH(ID1,ID2)) →
ACCEPTM(ID2)) .
- p 95, l 15:
- "alpha'' should be ``gamma''.
- p 98, Equation (6.17):
- 2^{k-m} should be 2^{k+1-m}-1. Bill Gasarch
points out the following simpler proof of this proposition which he
attributes to the book "Linear Orderings" by J. Rosenstein.
Proposition: Let A and B be line graphs with at least 2^{k+1}+1 vertices and
constants 0 and max for the leftmost and rightmost elements. Then Delilah
wins the k move game on A and B
Pf: By induction on k.
k=0: Both graphs have at least three vertices. Thus there is no edge from
0 to max in either graph and Delilah wins the 0 move game.
Assume true for k-1 and let's play the game for k. Think of both A and B
as being in three parts: first 2^{k}+1 points, middle part, last 2^{k}+1
points. (If the size of one of the graphs is exactly 2^{k+1}+1, then the
left and right parts intersect at a point and the middle part is that
intersecting point.)
KEY: once the first pair of moves is made A and B are both split into two
parts, and Delilah need only have a winning strategy on each part
separately.
Delilah's first move:
1) If Samson plays in the first part of A, say m points from the left,
then Delilah plays m points from the left in first part of B.
The game is now in two parts--- the stuff BEFORE the pebble and
the stuff AFTER.
The stuff before, in both A and B is the same graph, so the strategy there
is trivial. The stuff after the pebble has both parts at least 2^{k} +1,
so by induction Delilah has a winning strategy.
2) Similar if Samson plays in last part of A, or in first or last part of B.
3) If Samson plays middle part of either, then Delilah plays middle part
of the other. Both halves of the game are now inductively wins for Delilah.
QED
- p 102, Exercise 6.26, part 2:
- "log(n+2)" should be "log(n-2)",
"2r+1 -1" should be "2r+1 +1", and
"2r+2 -2" should be "2r+2 +2".
- p 103, line 12:
- "(r - m)" should be "(r - (m+1))".
- p 109, line 14:
- "Lk" should be "Lk".
- p 110, line 1:
- "at most d" should be "at least d".
- p 110, Exercise 6.44:
- "L2, etc." should
be "L2etc.".
- p 112, last paragraph:
- I wrote that, "In [my] opinion,
zero-one laws are inimical to computation."
Yuri Gurevich pointed out that I was wrong about this: Choiceless
Polynomial Time has a zero-one law [BG03] and the "Cai-Furer-Immerman"
property (Theorem 13.26) is expressible in Choiceless Polynomial Time [DRR05].
- p 116, line 11:
- "n's head" should be "N's head".
- p 117, first line of paragraph just above Corollary
7.10, and also first line just after Corollary 7.10:
- "Proposition 7.6" should be "Theorem 7.8".
- p 119, in the proof of Theorem 7.16 (SAT is NP complete), "D(e1, . . ., ek)" should be
"Δ(e1, . . ., ek)".
- p 139, line -4:
- Chandra and Harel defined the
fixed-point hierarchy for finite structures and asked whether it was strict
[CH80b].
- p 146-147:
- Item 5 and δ5 are repeats of item 3
and δ3. Instead, item 5 should be the case: α(\bar{u},
bar{w};x) ∧ ¬
α(\bar{u}, \bar{s};x): first α-edge found so store in
s. and δ5 should be modified accordingly.
- p 148, line 4:
- "β(w,j,w',j+1)" should be
"β(w,j+1,w',j)".
- p 148, lines 9 and 11:
- "l" should be
"L".
- p 149, Exercise 9.19:
- "REACH" should be "REACHd".
- p 150, line 17:
- "b ≤" should be "c ≤".
- p 153, line 16:
- The last two terms of the last clause, i.e., "
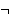 f1
f1 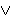
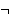 f2"
should be omitted. Also, the
"
f2"
should be omitted. Also, the
"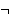 A(e)" on the previous line is unneeded.
A(e)" on the previous line is unneeded.
- p 155, lines 5 to 7:
- see also Leivant [Lei89] for a very
similar characterization of polynomial time as a restriction of
second-order logic.
- p 169, line -8:
- delete "of".
- p 176, Corollary 11.15:
- "SAT = REACHd" should be
"SAT ≤qfp REACH".
- p 176, lines 1-2:
- "a similar proposition holds where all
occurrences of the generalized quantifiers are positive." should be changed
to "the situation is more subtle, cf. [Ste94, Ste91]."
- p 191, line 4:
- "Samson" should be "Delilah".
- p 202, line -4:
- "Question 12.1 was first raised by Chandra
and Harel in [CH80b]. It remains quite open at this writing."
- p 245, line 17:
- "NP" should be "MATH"
- p 259, reference [Lu82]:
- name "Luks" is missing
Thanks to:
Jacob Arbib,
Argimiro Arratia,
Maya Bernhard,
David Benson,
Michaël Cadilhac
Jamie Cobleigh,
Creidieki Crouch,
Bill Gasarch,
Yuri Gurevich,
David Harel,
Bill Hesse,
Skip Jordan,
Daniel Leivant,
Steven Lindell,
Prabhu Manyem,
Greg Meredith,
Enrique Garcia Moreno Esteva,
Sebastian Mueller,
Martin Otto,
David Richerby,
Jeff Sarnat,
Bob Sloane,
Jerry Smith,
Ernst Specker,
Anthony Widjaja To,
Jan Van den Bussche,
and,
Philipp Weis
for pointing out corrections.
Please send me additional typos, errors,
comments, etc., thanks!
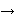 b
b 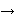 c" is equivalent to
"a
c" is equivalent to
"a 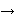 (b
(b 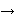 c)"
c)"
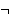 f1
f1 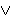
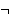 f2"
should be omitted. Also, the
"
f2"
should be omitted. Also, the
"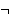 A(e)" on the previous line is unneeded.
A(e)" on the previous line is unneeded.