This assignment is due at the start of class on Thursday,
October 15. Mail it to
In this exercise, you will train probabilistic language models to distinguish between words in different languages. Rather than looking up whole words in a dictionary, you will build models of character sequences so you can make a guess about the language of unseen words. You will need to use NLTK and the Universal Declaration of Human Rights corpus.
Download the file udhr.py to your working directory. When you start python, run:
>>> execfile('udhr.py')
>>> dir()
['__builtins__', '__doc__', '__name__', 'english', 'english_dev', 'english_test', 'english_train', 'french', 'french_dev', 'french_test', 'french_train', 'italian', 'italian_dev', 'italian_test', 'italian_train', 'nltk', 'spanish', 'spanish_dev', 'spanish_test', 'spanish_train', 'udhr']
This shows that there are now training, development, and test
samples for English, French, Italian, and Spanish. The training
and development data are continuous strings of words; the test
data are lists of individual word strings for easier testing.
Build unigram, bigram, and trigram character models for
all four languages. You may find it convenient to use the NLTK
classes FreqDist
and ConditionalFreqDist, described in chapter 2 of
the NLTK book. If you models have free parameters, tune them on
the development data.
For each word in the English test sets, calculate the probability assigned to that string by English vs. French unigram models, E vs. F bigram models, and E vs. F trigram models. Don't forget to include the implicit space before and after each word. The number of times each model predicts English divided by the length of the word list (1000) is the accuracy of your model. Report the accuracies of the 1-, 2-, and 3-gram models.
Perform the same experiment for Spanish vs. Italian. Which language pair is harder to distinguish?
For this exercise, you will implement the dynamic program to
compute forward, backward, and Viterbi probabilities and the EM
algorithm for parameter estimation. You will use just the plain
English text in the english_train variable.
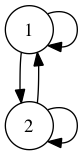
Learn the parameters of a simple two-state HMM from the
English training data. The hidden Markov process should be
fully connected, like so:

Each of the states, 1 and 2, should be capable of emitting any of the 2 * 26 + 4 punctuation and space characters of the alphabet, though with different probabilities. Randomly initialize the emission and transition probabilities to a uniform distribution plus a little noise. Without noise, EM will not be able to move in any direction.
Run the forward and backward procedures so that you can get the expected counts for each kind of transition and emission. Then re-estimate the probabilites of each using maximum likelihood count-and-normalize. Stop when the probabilities at the current iteration are identical to those of the previous one, or when you reach 500 iterations of EM.
After EM training converges, implement and run the Viterbi algorithm to assign a hidden state to each character in the training sequence. What patterns, if any, do you observe in this assignment?
Train a similar four-state and an eight-state HMM in the same way. What patterns do you observe in the Viterbi output?